题目内容
如图，AB是半圆O的直径，弦AD，BC相交于点P，且CD，AB的长分别是一元二次方程x2-7x+12=0的两根，则cos∠DPB=考点：圆周角定理,相似三角形的判定与性质,锐角三角函数的定义
专题：计算题
分析：先利用因式分解法解方程得到AB=4，CD=3，再根据圆周角定理得∠C=∠ABP，∠CDP=∠A，则可判断△PCD∽△PBA，利用相似的性质得
=
=
，
连接BD，如图，由AB是半圆O的直径得到∠ADB=90°，然后在Rt△PDB中根据余弦的定义求解．
| PD |
| PB |
| CD |
| AB |
| 3 |
| 4 |
连接BD，如图，由AB是半圆O的直径得到∠ADB=90°，然后在Rt△PDB中根据余弦的定义求解．
解答：
解：解方程x2-7x+12=0得x1=3，x2=4，则AB=4，CD=3，
∵∠C=∠ABP，∠CDP=∠A，
∴△PCD∽△PBA，
∴
=
=
，
连接BD，如图，
∵AB是半圆O的直径，
∴∠ADB=90°，
在Rt△PDB中，cos∠DPB=
=
．
故答案为
．
解：解方程x2-7x+12=0得x1=3，x2=4，则AB=4，CD=3，∵∠C=∠ABP，∠CDP=∠A，
∴△PCD∽△PBA，
∴
| PD |
| PB |
| CD |
| AB |
| 3 |
| 4 |
连接BD，如图，
∵AB是半圆O的直径，
∴∠ADB=90°，
在Rt△PDB中，cos∠DPB=
| PD |
| PB |
| 3 |
| 4 |
故答案为
| 3 |
| 4 |
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了相似三角形的判定与性质和锐角三角函数．
练习册系列答案
相关题目
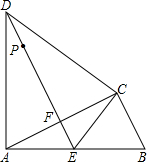如图，△ABC中，∠ACB=90°，以AC为一边在△ABC作等边三角形ACD，过点D作DE⊥AC，垂足为F，DE与AB相交于点E，连接CE．
如图，在Rt△ABC中，∠ACB=90°，AB=5，cosB=