题目内容
6．解下列二元一次方程组：（1）$\left\{\begin{array}{l}{66x+17y=3967}\\{25x+y=1247}\end{array}\right.$
（2）$\left\{\begin{array}{l}{80x-87y=2156}\\{22x-y=868}\end{array}\right.$
（3）$\left\{\begin{array}{l}{83x+64y=9291}\\{90x-y=3598}\end{array}\right.$．
分析 （1）方程组利用加减消元法求出解即可；
（2）方程组利用加减消元法求出解即可；
（3）方程组利用加减消元法求出解即可．
解答 解：（1）$\left\{\begin{array}{l}{66x+17y=3967①}\\{25x+y=1247②}\end{array}\right.$，
②×17-①得：359x=17232，
解得：x=48，
把x=48代入②得：y=47，
则方程组的解为$\left\{\begin{array}{l}{x=48}\\{y=47}\end{array}\right.$；
（2）$\left\{\begin{array}{l}{80x-87y=2156①}\\{22x-y=868②}\end{array}\right.$，
②×87-①得：1834x=73360，
解得：x=40，
把x=40代入②得：y=12，
则方程组的解为$\left\{\begin{array}{l}{x=40}\\{y=12}\end{array}\right.$；
（3）$\left\{\begin{array}{l}{83x+64y=9291①}\\{90x-y=3598②}\end{array}\right.$，
①+②×64得：5843x=239563，
解得：x=41，
把x=41代入②得：y=92，
则方程组的解为$\left\{\begin{array}{l}{x=41}\\{y=92}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
16．下列方程为一元一次方程的是（ ）
| A． | x+4=4-x2 | B． | x+y=-3x | C． | $\frac{1}{2x+3}=1$ | D． | 5-$\frac{1}{3}x=\frac{2}{3}x$ |
17．某小组参加植树活动，全组学生的植树数量如表所示，则该小组平均每人植树7株．
| 植树数量（株） | 5 | 6 | 7 | 8 |
| 人数（人） | 1 | 1 | 2 | 3 |
14．如图，点P在平面直角坐标系中按图中箭头方向运动，第一次从原点运动到点（1，1），第二次接着运动到点（2，0），第三次接着运动到点（3，2），…，按这样的运动规律，运动第2011次后的点坐标是 （ ）
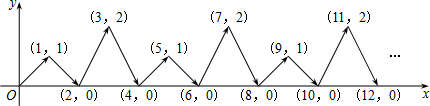
| A． | （2011，1） | B． | （2012，2） | C． | （2011，2） | D． | （2011，0） |
如图，在直角坐标系中，三角形ABC的三个顶点分别为A（-1，3）B（-4，1）C（-4，2）
如图是一个正方体的表面展示图，则原正方体中与“建”字所在面相对的面上标的字是汉．
15．点P1（1，3）与点P2关于原点对称，则P2的坐标是（ ）
| A． | （-5，-3） | B． | （1，-3） | C． | （-1，-3） | D． | （5，-3） |