题目内容
7．已知$\sqrt{5.217}$=2.284，$\sqrt{52.17}$=7.223，则$\sqrt{0.05217}$=0.2284，若$\sqrt{x}$=72，23，则x的值为5217．分析 根据算术平方根的定义，即可解答．
解答 解：由$\sqrt{5.217}$=2.284，$\sqrt{52.17}$=7.223，则$\sqrt{0.05217}$=$\sqrt{5.217×0.01}=\sqrt{5.217}×0.1$=2.284×0.1=0.2284．
若$\sqrt{x}$=72，23，则x的值为5217，
故答案为：0.2284，5217．
点评 本题考查了算术平方根，解决本题的关键是熟记算术平方根的定义．
练习册系列答案
相关题目
4．
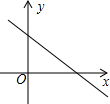一次函数y=kx+b的图象如图所示，则代数式|k-b|-$\sqrt{{k}^{2}}$可化简为（ ）
一次函数y=kx+b的图象如图所示，则代数式|k-b|-$\sqrt{{k}^{2}}$可化简为（ ）| A． | 2k-b | B． | b-2k | C． | -b | D． | b |
2．在实数范围内，下列结论正确的是（ ）
| A． | 若|a|=|b|，则a=b | B． | 若a2=b2，则a=b | C． | 若$\root{3}{-a}=\root{3}{b}$，则a=-b | D． | 若a2＞b2，则a＞b |
12．若$\sqrt{a+b+5}$+|2a-b+1|=0，则（b-a）2005的值为（ ）
| A． | -1 | B． | 1 | C． | 52005 | D． | -52005 |
19．把下列方程化成一般形式后，系数和为0的方程是（ ）
| A． | x2-2x+3=0 | B． | x2+2x-3=0 | C． | x2-4x-3=0 | D． | 2x2-5=3x |
17．若$\frac{x}{y}$=$\frac{3}{4}$，则$\frac{x+y}{y}$的值为（ ）
| A． | 1 | B． | $\frac{4}{7}$ | C． | $\frac{5}{4}$ | D． | $\frac{7}{4}$ |