题目内容
1.把抛物线y=-x2向左平移1个单位,则平移后抛物线的解析式为( )| A. | y=-(x-1)2 | B. | y=-(x+1)2 | C. | y=-x2+1 | D. | y=-x2-1 |
分析 先根据二次函数的性质得到抛物线y=-x2的顶点为(0,0),再利用点平移的规律得到点(0,0)平移后的对应点的坐标为(-1,0),然后根据顶点式写出平移后抛物线的解析式.
解答 解:抛物线y=-x2的顶点为(0,0),把点(0,0)向左平移1个单位所得对应点的坐标为(-1,0),所以平移后抛物线的解析式为y=-(x+1)2.
故选B.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 是二元一次方程mx+y=3的解,则m的值是__.
是二元一次方程mx+y=3的解,则m的值是__.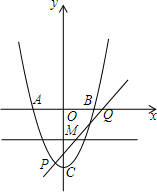 如图,抛物线y=x2-4分别交x轴于A、B,交y轴于C,P为第三象限的抛物线上一点,过P点的直线y=kx-3交直线y=-2于点M,交抛物线于另一点Q,若P、Q两点关于M成中心对称,求k的值.
如图,抛物线y=x2-4分别交x轴于A、B,交y轴于C,P为第三象限的抛物线上一点,过P点的直线y=kx-3交直线y=-2于点M,交抛物线于另一点Q,若P、Q两点关于M成中心对称,求k的值.