题目内容
17.有依次排列的3个数:3,9,8.对任意相邻的两个数.都用右边的数减去左边的数,所得之差写在这两个数之间.可产生一个新数串①:3,6,9,-1,8,这称为第1次操作:做第2次同样的操作后也可产生一个新数串②:3,3,6,3,9,-10,-1,9,8…依次操作下去.(1)数串①的所有数之和为25,数串②的所有数之和为30;第3次操作以后所产生的新数串③为3,0,3,3,6,-3,3,6,9,-19,-10,9,-1,10,9,-1,8,,所有数之和为35.
(2)操作第100次产生的新数串的所有数之和是多少?
分析 根据题意,计算可得第1次操作后所得数串为:3,6,9,-1,8;进而可得第2次操作后所得数串;…分析可得其和的规律规律,运用规律可得答案.
解答 解:(1)原数串为3个数:3,9,8,所有数之和为20;
第1次操作后所得数串为:
3,6,9,-1,8,所有数之和为25;
第2次操作后所得数串为:
3,3,6,3,9,-10,-1,9,8,所有数之和为30;
第3次操作后所得数串为:
3,0,3,3,6,-3,3,6,9,-19,-10,9,-1,10,9,-1,8,所有数之和为3,5;
(2)由上面可以看出,每一次操作后所得新数串所有数的和比上一次增加5,
操作第100次产生的新数串的所有数之和是(3+9+8)+100×5=520.
点评 此题考查数字的变化规律,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
相关题目
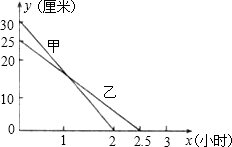 在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息回答下列问题
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息回答下列问题 在图示的直角坐标系中分别作出y=-2x与y=-2x+3的图象,并说出两个图象之间的关系,以及各自函数图象的特点.
在图示的直角坐标系中分别作出y=-2x与y=-2x+3的图象,并说出两个图象之间的关系,以及各自函数图象的特点. 如图,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BD=CD.求证:DE是⊙O的切线.
如图,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BD=CD.求证:DE是⊙O的切线.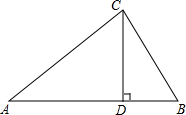 如图,在R△ABC中,∠ACB=90°,CD⊥AB,AC=5,CD=3,求BC.
如图,在R△ABC中,∠ACB=90°,CD⊥AB,AC=5,CD=3,求BC.