Question

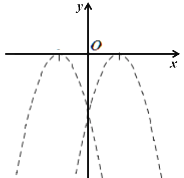
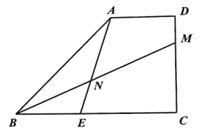
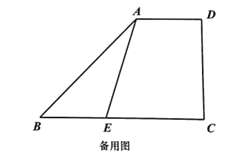
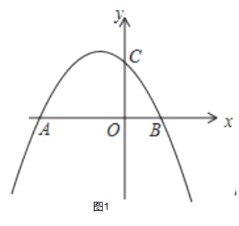
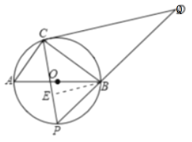
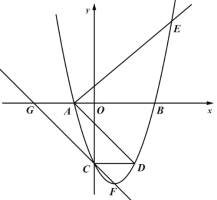
【题目】如图，二次函数（其中）的图象与x轴分别交于点A、B（点A位于B的左侧），与y轴交于点C，过点C作x轴的平行线CD交二次函数图像于点D．

（1）当m2时，求A、B两点的坐标；

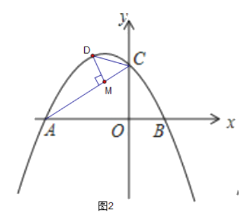
（2）过点A作射线AE交二次函数的图像于点E，使得BAEDAB．求点E的坐标（用含m的式子表示）；

（3）在第（2）问的条件下，二次函数的顶点为F，过点C、F作直线与x轴于点G，试求出GF、AD、AE的长度为三边长的三角形的面积（用含m的式子表示）．

Answer 1

【答案】（1），；（2）；（3）

【解析】

（1）求图象与x轴交点，即函数y值为零，解一元二次方程即可;

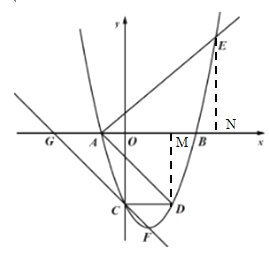
（2）过作轴，过作轴，先求出D点坐标为，设E点为，即可列等式求m的值得E点坐标；

（3）由直线的方程：，得G点坐标，再用m的表达式分别表达GF、AD、AE即可.

（1） 当时，，

∵图象与x轴分别交于点A、B

∴时，

∴，

（2）∵，轴

∴

过作轴，过作轴

∵

∴

设E

∴

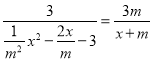
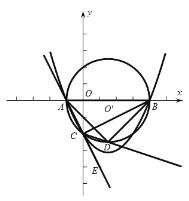
（3）以GF、BD、BE的长度为三边长的三角形是直角三角形.理由如下：

二次函数的顶点为F,则F的坐标为(m,4)，过点F作FH⊥x轴于点H.

∵tan∠CGO=，tan∠FGH=，

∴=，

∴=，

∵OC=3，HF=4，OH=m，

∴，

∴OG=3m.

∴

，

∴

∴、、能构成直角三角形面积是

所以、、能构成直角三角形面积是