题目内容
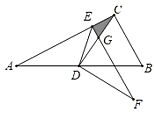
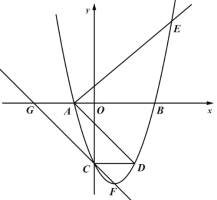
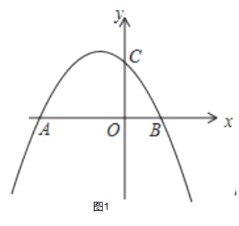
【题目】如图1,二次函数![]() 的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0)
的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0)
(1)b= ,点B的坐标是 ;
(2)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由
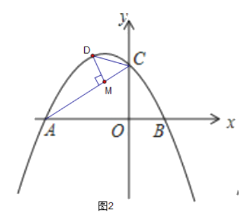
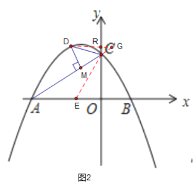
(3)如图2,点D是抛物线上第二象限内的一动点,过点D作DM⊥AC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠BAC的2倍?若存在,写出点D的横坐标;若不存在,请说明理由
【答案】(1)﹣![]() ,(
,(![]() ,0);(2)∠CBA=2∠CAB,见解析;(3)存在,-1与
,0);(2)∠CBA=2∠CAB,见解析;(3)存在,-1与![]()
【解析】
(1)把点A的坐标,代入函数解析式可求出b的值,代入y=0求出x值,进而可得出点B的坐标;
(2)作∠CBA的角平分线,交y轴于点E,过点E作EF⊥BC于点F,设OE=n,则CE=2-n,EF=n,利用面积法可求出n值,进而可得出![]() =
=![]() =
=![]() ,结合∠AOC=90°=∠BOE可证出△AOC∽△BOE,根据相似三角形的性质可得出∠CAO=∠EBO,再根据角平分线的性质可得出∠CBA=2∠EBO=2∠CAB,此题得解;
,结合∠AOC=90°=∠BOE可证出△AOC∽△BOE,根据相似三角形的性质可得出∠CAO=∠EBO,再根据角平分线的性质可得出∠CBA=2∠EBO=2∠CAB,此题得解;
(3)过点D作DR⊥y垂足为R,DR交AC与点G,在AB上找点E使![]() ,分当
,分当![]() =2
=2![]() 时和当
时和当![]() =2
=2![]() 时两种情况讨论.
时两种情况讨论.
(1)把A(﹣4,0)代入![]() 得,
得,
∴﹣![]() ﹣4b+2=0,
﹣4b+2=0,
∴b=﹣![]() .
.
当y=0时,有![]() ,
,
解得:x1=﹣4,x2=![]() ,
,
∴点B的坐标为(![]() ,0).
,0).
故答案为:﹣![]() ;(
;(![]() ,0).
,0).
(2)∠CBA=2∠CAB,理由如下:
作∠CBA的角平分线,交y轴于点E,过点E作EF⊥BC于点F,如图所示.
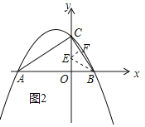
∵点B(![]() ,0),点C(0,2),
,0),点C(0,2),
∴OB=![]() ,OC=2,BC=
,OC=2,BC=![]() .
.
设OE=n,则CE=2﹣n,EF=n,
由面积法,可知:![]() OBCE=
OBCE=![]() BCEF,即
BCEF,即![]() (2﹣n)=
(2﹣n)=![]() n,
n,
解得:n=![]() .
.
∵![]() =
=![]() =
=![]() ,∠AOC=90°=∠BOE,
,∠AOC=90°=∠BOE,
∴△AOC∽△BOE,
∴∠CAO=∠EBO,
∴∠CBA=2∠EBO=2∠CAB
(3)如图所示:过点D作DR⊥y垂足为R,DR交AC与点G,在AB上找点E使![]() , 则DG∥AB,∠G=∠BAC,∠CEO=2∠BAC,
, 则DG∥AB,∠G=∠BAC,∠CEO=2∠BAC,
∵A(-4,0),B(![]() ,0),C(0,2),
,0),C(0,2),
在直角三角形EOC中,![]()
即:![]()
解得:OE=![]()
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
设D![]() ,
,
当![]() =2
=2![]() 时,
时,
∵∠MCD=∠CDG+∠G
∴![]() =
=![]() ,
,
∴![]()
则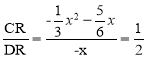
解得:![]() =0(不符合题意,舍去),
=0(不符合题意,舍去),![]() =-1,
=-1,
∴点D的横坐标是-1
当![]() =2
=2![]() 时,则∠CDM=∠CEO
时,则∠CDM=∠CEO
∴![]()
设CM=4k,DM=3k,则CD=5k,
![]() =
=![]() ,则MG=6k,DG=
,则MG=6k,DG=![]() ,CG=2k,
,CG=2k,
∵AC=![]()
∴![]()
∴CR=![]() ,
,![]() ,
, ![]()
![]() ,
,
∴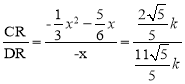 ,
,
解得:![]() =0(不符合题意,舍去),
=0(不符合题意,舍去),![]() =
=![]() ,
,
点D的横坐标是![]()
综上所述,点D的横坐标是-1或![]()

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案