题目内容
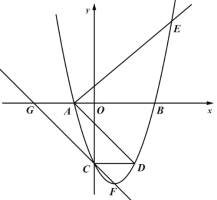
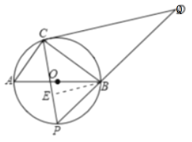
【题目】如图,直径![]() 把圆
把圆![]() 分为两个半圆,一个半圆弧上有一定点
分为两个半圆,一个半圆弧上有一定点![]() ,另一半圆弧上有一动点
,另一半圆弧上有一动点![]() .过
.过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]()
(2)若![]() ,
,![]()
①当点![]() 运动到半圆弧
运动到半圆弧![]() 中点时,求
中点时,求![]() 边
边![]() 上的高;
上的高;
②当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积最大?并求这个最大面积
的面积最大?并求这个最大面积![]() .
.
【答案】(1)证明见解析;(2)①![]() ,
,![]() ;②当PC=10时,
;②当PC=10时,![]() .
.
【解析】
(1)易知![]() ,
,![]() ,证明
,证明![]() 即可.
即可.
(2)①当点![]() 运动到半圆弧
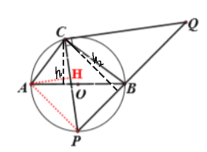
运动到半圆弧![]() 中点时,连接AP,过点A作AH⊥PC,由圆周角定理知
中点时,连接AP,过点A作AH⊥PC,由圆周角定理知![]() ,得到
,得到![]() ,
,![]() ,根据勾股定理在
,根据勾股定理在![]() 中
中![]() ,从而得到
,从而得到![]() ,利用等积法求得
,利用等积法求得![]() 的斜边PC上的高
的斜边PC上的高![]() ,再根据
,再根据![]() 的性质,得到PQ上的高
的性质,得到PQ上的高![]() 的值;
的值;
②因点![]() 运动过程中,
运动过程中,![]() 恒成立,而
恒成立,而![]() 面积为定值,根据
面积为定值,根据![]() ,得到
,得到![]() ,故当QC最大为直径时,
,故当QC最大为直径时,![]() 最大.问题得解.
最大.问题得解.
(1)证明:∵![]() 是直径∴
是直径∴![]()
又∵![]() ,∴
,∴![]()
又∵![]() ∴
∴![]() ∴
∴![]()
∴![]()
(2)①解:由直径![]() ,
,![]() 可得
可得![]() ,
,![]()
∵点![]() 在半圆弧
在半圆弧![]() 的中点∴
的中点∴![]() ,
,![]()
过![]() 作
作![]() 于
于![]() ,在
,在![]() 中
中![]()
∴![]() ∴
∴![]()
在![]() 中
中![]()
∴![]()
设![]() 斜边上高为
斜边上高为![]() ,
,![]() 斜边上高为
斜边上高为![]()
![]() 得
得![]()
∵![]() ∴
∴![]()
∴![]()
②解:在点![]() 运动过程中,
运动过程中,![]() 恒成立
恒成立
∴当![]() 最大时,
最大时,![]() 面积最大
面积最大
∵![]() 直径
直径![]()
此时,![]() ,可得,
,可得,![]()
∴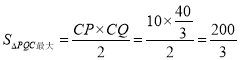

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目