题目内容
19. 如图,在平面直角坐标系中,等腰Rt△ABC中,∠ABC=90°,点E是点C关于点B的对称点,A(0,3),B(-1,0),则点E的坐标是(2,-1).
如图,在平面直角坐标系中,等腰Rt△ABC中,∠ABC=90°,点E是点C关于点B的对称点,A(0,3),B(-1,0),则点E的坐标是(2,-1).
分析 首先作CD⊥x轴于点D,证得△CDB≌△BOA,得出点C的坐标,进一步利用对称点的坐标求法得出E点的坐标即可.
解答 解:如图,
∵△ABC是等腰直角三角形,
∴BC=BA,∠ABC=90°,
∵∠CBD+∠ABO=∠CBD+∠DCB=90°,
∴∠ABO=∠DCB,
在△CDB和△BOA中,
$\left\{\begin{array}{l}{∠CDB=∠AOB=90°}\\{∠DCB=∠ABO}\\{BC=BA}\end{array}\right.$,
∴△CDB≌△BOA,
∴CD=OB=1,BD=OA=3,
∴点C的坐标为(-3,1),
∵点E是点C关于点B的对称点,
∴点E的坐标为(2,-1).
故答案为:(2,-1).
点评 此题考查三角形全等的判定与性质,等腰直角三角形的性质,关于一点对称点的坐标特征,借助直角坐标系的特点,灵活作出辅助线解决问题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
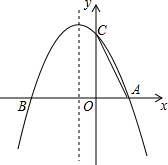 如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
如图,已知抛物线y=ax2+bx+c与x轴交于A(m,0),B(n,0),点A位于点B的右侧,且m,n是一元二次方程x2+2x-3=0的两个根,与y轴交于C(0,3).在抛物线上的对称轴上是否存在点P,使得△PAC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
 已知:如图,AC、BD交于点O,且OA=OC,OB=OD,求证:AB∥CD,AD∥BC.
已知:如图,AC、BD交于点O,且OA=OC,OB=OD,求证:AB∥CD,AD∥BC.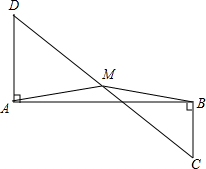 已知,如图,DA⊥AB,CB⊥AB,M是DC的中点,求证:MA=MB.
已知,如图,DA⊥AB,CB⊥AB,M是DC的中点,求证:MA=MB.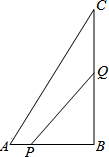 如图,在△ABC中∠B=90°,AB=7cm,BC=12cm,点P从点A开始沿AB边向点B以1cm的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,一点到达,另一点立即停止运动.如果P,Q分别从A,B同时出发,经几秒钟,使△PBQ的面积等于10cm2?
如图,在△ABC中∠B=90°,AB=7cm,BC=12cm,点P从点A开始沿AB边向点B以1cm的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,一点到达,另一点立即停止运动.如果P,Q分别从A,B同时出发,经几秒钟,使△PBQ的面积等于10cm2?