题目内容
17.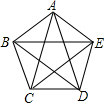 如图:正五边形ABCDE中,若边长AB=2,则AC为( )
如图:正五边形ABCDE中,若边长AB=2,则AC为( )| A. | $\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$+2 | D. | $\sqrt{5}$-2 |
分析 如图设AC与BD交于点O.首先证明AB=OA=2,设CO=x,再证明△BCO∽△ACB,可得$\frac{CB}{AC}$=$\frac{CO}{CB}$,即BC2=CO•CA,列出方程即可解决问题.
解答 解:如图设AC与BD交于点O.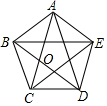
在正五边形ABCD中,易知∠CBO=∠CAB=36°,∠ABO=∠AOB=72°,
∴BC=AB=AO=2,设CO=x,
∵∠BCO=∠BCA,
∴△BCO∽△ACB,
∴$\frac{CB}{AC}$=$\frac{CO}{CB}$,
∴BC2=CO•CA,
∴4=x(x+2),
∴x=$\sqrt{5}$-1或-$\sqrt{5}$-1(舍弃),
∴AC=OC+OA=$\sqrt{5}$+1.
故选A.
点评 本题考查正多边形与圆、等腰三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形,列出方程解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列运算正确的是( )
| A. | 20=0 | B. | a•2a=3a | C. | (ab2)3=3a3b6 | D. | 2a6÷a-2=2a8 |
12.要使方程x2-mx+m=-1有实数根,实数m的值可以是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 5 |
2.月球到地球的距离约384000千米,它的长度用科学记数法表示为多少米?( )
| A. | 0.384×109 | B. | 3.84×108 | C. | 3.84×107 | D. | 3.84×105 |
9.点P(-6,1)关于x轴对称的点的坐标是( )
| A. | (-6,-1) | B. | (1,-6) | C. | (6,1) | D. | (6,-1) |
6.-$\frac{5}{3}$的倒数的相反数是( )
| A. | $\frac{5}{3}$ | B. | -$\frac{5}{3}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
7.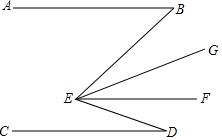 已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )
已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )
 已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )
已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 20° |