题目内容
19.已知等腰△ABC,AB=AC,∠ABC=20°,P为直线BC上一点,BP=AB,则∠PAC的度数为60°或150°.分析 如图1,根据等腰三角形的性质和三角形的内角和得到∠C=∠B=20°,∠BAC=140°,由等腰三角形的性质得到∠BAP=$\frac{180°-20°}{2}$=80°,于是求得∠PAC=60°,如图2,同理求得∠P=∠PAB=$\frac{1}{2}∠$ABC=10°,于是求得∠PAC=150°.
解答 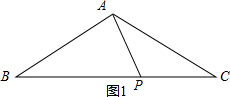 解:如图1,∵AB=AC,∠ABC=20°,
解:如图1,∵AB=AC,∠ABC=20°,
∴∠C=∠B=20°,
∴∠BAC=140°,
∵BP=AB,
∴∠BAP=$\frac{180°-20°}{2}$=80°,
∴∠PAC=60°,
如图2,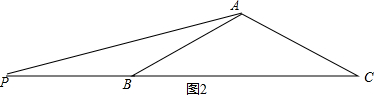 ∵AB=AC,∠ABC=20°,
∵AB=AC,∠ABC=20°,
∴∠C=∠B=20°,
∴∠BAC=140°,
∵BP=AB,
∴∠P=∠PAB=$\frac{1}{2}∠$ABC=10°,
∴∠PAC=150°.
综上所述:∠PAC的度数为60°或150°,
故答案为:60°或150°.
点评 本题考查了等腰三角形的性质,三角形的外角的性质,三角形的内角和,正确的画出图形是解题的关键.

练习册系列答案
相关题目
7.若n边形共有54条对角线,则n的值是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
8.下列图形:线段、角、圆、平行四边形、矩形、正方形中,既是轴对称图形又是中心对称图形的有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
 如图所示,要使图中平面展开图按虚线折叠成正方体后相对面上两个数之和相等,则b-c=-7.
如图所示,要使图中平面展开图按虚线折叠成正方体后相对面上两个数之和相等,则b-c=-7.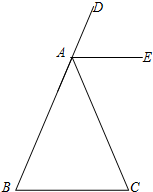 如图,△ABC中,AB=AC,AE是外角∠DAC的角平分线.
如图,△ABC中,AB=AC,AE是外角∠DAC的角平分线. 若二次函数y=ax2+bx+c的图象如图所示,则它的对称轴是x=3.
若二次函数y=ax2+bx+c的图象如图所示,则它的对称轴是x=3.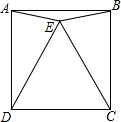 如图,四边形ABCD是正方形,△CDE是等边三角形,若AE=4cm,则S△AEB=4cm2.
如图,四边形ABCD是正方形,△CDE是等边三角形,若AE=4cm,则S△AEB=4cm2.