题目内容
在等边△ABC中,∠ABC,∠ACB的平分线交于点O,若OB,OC的垂直平分线交BC于点E,F,猜想EF与AB之间的数量关系,并加以证明.
考点:等边三角形的判定与性质,线段垂直平分线的性质
专题:
分析:连接OE,OF,根据线段的垂直平分线的性质得出OE=EB,OF=FC,根据角的平分线的性质得出∠OBE=∠OEB=30°,进而得出∠OEF=60°,∠OFE=60°得出△OEF是等边三角形,得出BE=EF=FC,即可得出EF=
AB.
| 1 |
| 3 |
解答: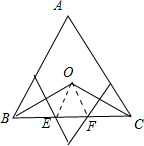 证明:连接OE,OF.
证明:连接OE,OF.
∵若OB,OC的垂直平分线交BC于点E,F
∵OE=EB,OF=FC
∵△ABC是等边三角形,角ABC,角ACB的平分线交于点O
∴∠OBE=∠OEB=30°,
∴∠OEF=60°
同理∠OFE=60°
∴△OEF是等边三角形
∴BE=EF=FC
∴EF=
AB,
 证明:连接OE,OF.
证明:连接OE,OF.∵若OB,OC的垂直平分线交BC于点E,F
∵OE=EB,OF=FC
∵△ABC是等边三角形,角ABC,角ACB的平分线交于点O
∴∠OBE=∠OEB=30°,
∴∠OEF=60°
同理∠OFE=60°
∴△OEF是等边三角形
∴BE=EF=FC
∴EF=
| 1 |
| 3 |
点评:本题考查了等边三角形的判定和性质,线段垂直平分线的性质,得出△OEF是等边三角形是本题的关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
在△ABC中,CA=CB,以△ABC的边BC向外侧作正方形BCDE,若记∠DAB的度数为α,则关于α的值下列说法正确的是( )
| A、视△ABC而定 |
| B、α<∠CAB |
| C、45°<α<90° |
| D、与△ABC形状无关 |
下列方程中,关于x的一元二次方程是( )
| A、(x+1)2=2(x+1) | ||||
B、
| ||||
| C、ax2+bx+c=0 | ||||
| D、x2+2x=x2-1 |