题目内容
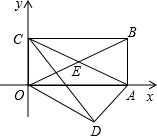 如图,把矩形纸片OABC放入直角坐标系中,是OA、OC分别落在x轴、y轴的正半轴上,连接AC将△ABC翻折,点B落在该坐标系平面内.设这个落点为点D,CD交x轴于E,已知CB=4,AB=2.
如图,把矩形纸片OABC放入直角坐标系中,是OA、OC分别落在x轴、y轴的正半轴上,连接AC将△ABC翻折,点B落在该坐标系平面内.设这个落点为点D,CD交x轴于E,已知CB=4,AB=2.(1)求点E的坐标和△ACE的面积;
(2)求点D的坐标,并判断点(4,-2)是否在直线OD上,说明理由;
(3)点P(-1,n),△PDC为直角三角形,求点P的坐标.
考点:一次函数综合题
专题:
分析:(1)首先证明△ACE是等腰三角形,在直角△OCE中利用勾股定理即可求得OE的长,求得E的坐标,进而求得△ACE的面积;
(2)作DF⊥x轴于点F,根据△ADE的面积求得D的纵坐标,然后在直角△ADF中,利用勾股定理求得AF的长,从而求得OF,即可得到D的坐标,然后利用待定系数法求得直线CD的解析式,然后把点(4,-2)代入判断即可;
(3)分∠PCD和∠CDP以及∠CPD是直角,三种情况进行讨论,从而求解.
(2)作DF⊥x轴于点F,根据△ADE的面积求得D的纵坐标,然后在直角△ADF中,利用勾股定理求得AF的长,从而求得OF,即可得到D的坐标,然后利用待定系数法求得直线CD的解析式,然后把点(4,-2)代入判断即可;
(3)分∠PCD和∠CDP以及∠CPD是直角,三种情况进行讨论,从而求解.
解答:解:(1)∵矩形OABC中,BC∥OA,
∴∠BCA=∠CAO,
又∵∠BCA=∠ACD,
∴∠ACD=∠CAO,
∴CE=AE,
设CE=AE=x,则OE=4-x,在直角△OCE中,OC2+OE2=CE2,则22+(4-x)2=x2,
解得:x=
,
则OE=4-
=
,则E的坐标是(
,0).
则S△ACE=
×
×2=
;
(2)作DF⊥x轴于点F.
S△ACD=S△ABC=
×4×2=4,
则S△ADE=4-
=
,
又∵S△ADE=
AE•DF,则
×
•DF=
,
∴DF=
,
在直角△ADF中,AF=
=
=
,
则OF=4-
=
,
则D的坐标是(
,-
),
设直线OD的解析式是y=kx,则
k=-
,解得:k=-
,
则直线OD的解析式是:y=-
x,
当x=4时,y=-2,则(4,-2)在直线OD上;
(3)当∠PCD是直角时,设PC的解析式是y=2x+a,把(0,2)代入解析式得:a=2,
则PC的解析式是y=2x+2,
当x=-1时,y=0,则P的坐标是(-1,0);
当∠CDP是直角时,设DP的解析式是y=2x+b,把(
,-
)代入得:b=-6,
则直线PD的解析式是y=2x-6,
当x=-1时,y=-8,则P的坐标是(-1,-8);
当∠CPD是直角时,设P的坐标是(-1,n),PC2=1+(2-n)2,CD2=(
)2+(-
-2)2=106,
PD2=(
+1)2+(-
-n)2,
∵PC2+PD2=CD2,
则1+(2-n)2+(
+1)2+(-
-n)2=106,
解得:n=
.
则P的坐标是(-1,
)或(-1,
)或(-1,-8)或(-1,0).
∴∠BCA=∠CAO,
又∵∠BCA=∠ACD,
∴∠ACD=∠CAO,
∴CE=AE,
设CE=AE=x,则OE=4-x,在直角△OCE中,OC2+OE2=CE2,则22+(4-x)2=x2,
解得:x=
| 5 |
| 2 |
则OE=4-
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |

则S△ACE=
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
(2)作DF⊥x轴于点F.
S△ACD=S△ABC=
| 1 |
| 2 |
则S△ADE=4-
| 5 |
| 2 |
| 3 |
| 2 |
又∵S△ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
∴DF=
| 6 |
| 5 |
在直角△ADF中,AF=
| AD2-DF2 |
22-(
|
| 8 |
| 5 |
则OF=4-
| 8 |
| 5 |
| 12 |
| 5 |
则D的坐标是(
| 12 |
| 5 |
| 6 |
| 5 |

设直线OD的解析式是y=kx,则
| 12 |
| 5 |
| 6 |
| 5 |
| 1 |
| 2 |
则直线OD的解析式是:y=-
| 1 |
| 2 |
当x=4时,y=-2,则(4,-2)在直线OD上;
(3)当∠PCD是直角时,设PC的解析式是y=2x+a,把(0,2)代入解析式得:a=2,
则PC的解析式是y=2x+2,
当x=-1时,y=0,则P的坐标是(-1,0);
当∠CDP是直角时,设DP的解析式是y=2x+b,把(
| 12 |
| 5 |
| 6 |
| 5 |
则直线PD的解析式是y=2x-6,
当x=-1时,y=-8,则P的坐标是(-1,-8);
当∠CPD是直角时,设P的坐标是(-1,n),PC2=1+(2-n)2,CD2=(
| 12 |
| 5 |
| 6 |
| 5 |
PD2=(
| 12 |
| 5 |
| 6 |
| 5 |
∵PC2+PD2=CD2,
则1+(2-n)2+(
| 12 |
| 5 |
| 6 |
| 5 |
解得:n=
2±4
| ||
| 5 |
则P的坐标是(-1,
2+4
| ||
| 5 |
2-4
| ||
| 5 |
点评:本题考查了待定系数法求函数的解析式,以及图形的折叠和勾股定理,正确进行讨论是关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
下列函数中,图象经过点(
,-4)的反比例函数是( )
| 1 |
| 2 |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
下列各组数是勾股数的是( )
| A、12、15、18 |
| B、0.3、0.4、0.5 |
| C、1.5、3、2.5 |
| D、12、16、20 |
在0,2,-3,-2这四个数中,最小的数是( )
| A、0 | B、2 | C、-3 | D、-2 |

 如图,点O在直线AC上,∠AOB=80°,OD平分∠BOC,求∠BOC,∠BOD,∠AOD的度数.
如图,点O在直线AC上,∠AOB=80°,OD平分∠BOC,求∠BOC,∠BOD,∠AOD的度数. 如图,把它折叠成正方体后三组对面上的两个数之和相等,则x=
如图,把它折叠成正方体后三组对面上的两个数之和相等,则x=