题目内容
如图，点O在直线AC上，∠AOB=80°，OD平分∠BOC，求∠BOC，∠BOD，∠AOD的度数．考点：角平分线的定义
专题：
分析：利用角平分线的定义以及邻补角的性质求出即可．
解答：解：∵∠AOB=80°，OD平分∠BOC，
∴∠BOC=180°-80°=100°，∠BOD=∠COD=
×100°=50°，
∴∠AOD=80°+50°=130°．
∴∠BOC=180°-80°=100°，∠BOD=∠COD=
| 1 |
| 2 |
∴∠AOD=80°+50°=130°．
点评：此题主要考查了角平分线的定义以及邻补角的定义，正确把握角平分线的定义是解题关键．
练习册系列答案
考前必练系列答案
相关题目
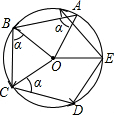如图所示，小范从一个圆形场地的A点出发，沿着与半径OA夹角为α的方向行走，走到场地边缘B后，再沿着与半径OB夹角为α的方向折向行走．按照这种方式，小范第五次走到场地边缘时处于弧AB上，此时∠AOE=48°，则α的度数是（ ）| A、60° | B、51° |
| C、48° | D、76° |
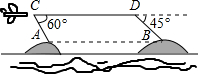某海域有两个海拔均为200米的海岛A和海岛B，一勘测飞机在距离海平面垂直高度为1100米的空中飞行，飞行到点C处时测得你正前方一海岛顶端A的俯角是60°，然后沿平行与AB的方向水平飞行1.99×104米到达点D处，在D处测得正前方另一海岛顶端B的俯角是45°，求两海岛间的距离AB．
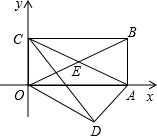如图，把矩形纸片OABC放入直角坐标系中，是OA、OC分别落在x轴、y轴的正半轴上，连接AC将△ABC翻折，点B落在该坐标系平面内．设这个落点为点D，CD交x轴于E，已知CB=4，AB=2．二次函数y=2x2-4x+m的图象上有点A（2013，a），B （2014，b），关于a，b的大小关系，下列正确的是（ ）
| A、a＞b |
| B、a＜b |
| C、a=b |
| D、m的取值不确定，无法确定a，b的大小 |
下列函数是反比例函数的是（ ）
A、y=
| ||||
| B、y=x2+x | ||||
C、y=
| ||||
| D、y=4x+8 |
圆内接四边形ABCD的四个内角之比可能是（ ）
| A、1：2：3：4 |
| B、1：3：4：5 |
| C、2：3：4：5 |
| D、2：3：5：4 |
已知二次函数y=a（x-1）2-b（a≠0）有最小值
，则a、b的大小比较为（ ）
| 1 |
| 2 |
| A、a＞b | B、a＜b |
| C、a=b | D、不能确定 |