题目内容
1.求$\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{…}}}}}}$-$\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+…}}}}}$的值.分析 设x=$\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{…}}}}}}$,y=$\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+…}}}}}$,两边平方得出关于x、y的方程求得方程的解,进一步得出答案即可.
解答 解:设x=$\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{…}}}}}}$,y=$\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+…}}}}}$,
则x2=2x,y2=2+y,
解得:x=2或x=0(舍去),y=2或y=-1(舍去)
因此$\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{2\sqrt{…}}}}}}$-$\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2+…}}}}}$=x-y=0.
点评 此题考查二次根式的化简求值,把问题转化为解方程是解决问题的关键.

练习册系列答案
相关题目
16.方程$\frac{2x}{x-1}$=1+$\frac{1}{x-1}$的解是( )
| A. | x=-1 | B. | x=0 | C. | x=1 | D. | x=2 |
13.下列说法中,正确的是( )
| A. | x=5是方程x+5=0的解 | B. | y=5是3y+15=0的解 | ||
| C. | z=-1是-$\frac{z}{4}$=4的解 | D. | x=0.04是方程25x=1的解 |
9.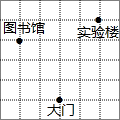 如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
 如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )| A. | (1,5) | B. | (-2,3) | C. | (-2,-1) | D. | (-2,1) |
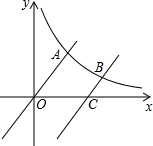 如图,已知函数y=x与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{k}{x}$交于点B,与x轴交于点C.
如图,已知函数y=x与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{k}{x}$交于点B,与x轴交于点C.