题目内容
如图，∠BAC=90°，EF∥BC，∠1=∠B，则∠DEC=________度．
90
分析：先利用平行线的性质和已知条件，推出∠B与∠EDC相等，得到ED与AB平行，再根据平行线的性质，即可得到∠DEC等于∠BAC等于90°．
解答：∵EF∥BC，
∴∠1=∠EDC，
又∵∠1=∠B，
∴∠EDC=∠B，
∴DE∥AB，
∴∠DEC=∠BAC=90°；
故应填90．
点评：解此题要首先根据平行线的性质结合已知条件进行等量代换，发现新的平行线，再运用平行线的性质求出要求的角．
分析：先利用平行线的性质和已知条件，推出∠B与∠EDC相等，得到ED与AB平行，再根据平行线的性质，即可得到∠DEC等于∠BAC等于90°．
解答：∵EF∥BC，
∴∠1=∠EDC，
又∵∠1=∠B，
∴∠EDC=∠B，
∴DE∥AB，
∴∠DEC=∠BAC=90°；
故应填90．
点评：解此题要首先根据平行线的性质结合已知条件进行等量代换，发现新的平行线，再运用平行线的性质求出要求的角．
练习册系列答案
名校课堂系列答案
相关题目
如图，∠BAC=90°，AD⊥BC，△ABE，△ACF都是等边三角形，则S△ABE：S△ACF等于（ ）| A、AB：AC | B、AD2：DC2 | C、BD2：DC2 | D、AC2：AB2 |
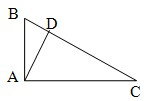6、如图，∠BAC=90°，AD⊥BC，则图中互余的角有（ ）
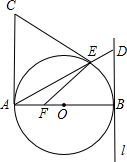直线AE与l相交于点D．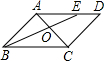
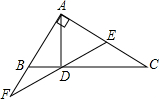
已知：如图，∠BAC=90°，∠C=30°，AD⊥BC于D，DE⊥AB于E，BE=1，BC=