题目内容
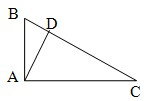6、如图，∠BAC=90°，AD⊥BC，则图中互余的角有（ ）分析：此题直接利用直角三角形两锐角之和等于90°的性质即可顺利解决．
解答：解：∵∠BAC=90°
∴∠B+∠C=90°①；
∠BAD+∠CAD=90°②；
又∵AD⊥BC，
∴∠BDA=∠CDA=90°，
∴∠B+∠BAD=90°③；
∠C+∠CAD=90°④．
故共4对．
故选C．
∴∠B+∠C=90°①；
∠BAD+∠CAD=90°②；
又∵AD⊥BC，
∴∠BDA=∠CDA=90°，
∴∠B+∠BAD=90°③；
∠C+∠CAD=90°④．
故共4对．
故选C．
点评：根据互余定义，找到和为90°的两个角即可．
练习册系列答案
相关题目
如图，∠BAC=90°，AD⊥BC，△ABE，△ACF都是等边三角形，则S△ABE：S△ACF等于（ ）| A、AB：AC | B、AD2：DC2 | C、BD2：DC2 | D、AC2：AB2 |
直线AE与l相交于点D．
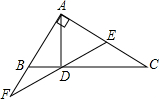
已知：如图，∠BAC=90°，∠C=30°，AD⊥BC于D，DE⊥AB于E，BE=1，BC=