题目内容
在△ABC中，∠C=90°，AC=3，AB=5，则sinA的值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：锐角三角函数的定义
专题：
分析：首先利用勾股定理求得BC的长度，然后利用锐角三角函数的定义进行解答．
解答：
解：∵在△ABC中，∠C=90°，AC=3，AB=5，
∴由勾股定理，得
BC=
=
=4．
∴sinA=
=
．
故选：B．
解：∵在△ABC中，∠C=90°，AC=3，AB=5，∴由勾股定理，得
BC=
| AB2-AC2 |
| 52-32 |
∴sinA=
| BC |
| AB |
| 4 |
| 5 |
故选：B．
点评：本题考查了正弦的定义：在直角三角形中，一锐角的正弦等于这个角的对边与斜边的比值．
练习册系列答案
相关题目
想象一下，将如图的盒子展开成为一个十字型图形，展开后得到的图形是（ ）A、 |
B、 |
C、 |
D、 |
如图，∠AOB=∠COD，若∠AOD=110°，∠BOC=70°，则以下结论正确的个数为（ ）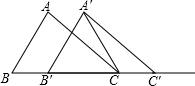
如图，△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC方向平移2个单位后，得到△A′B′C′，连结A′C，则△A′B′C的周长为（ ）
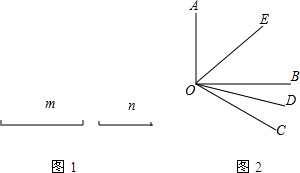（1）尺规作图（不写作法，保留作图痕迹）已知：如图1，线段m，n．求作：线段AB=m+2n．
如图，OM平分∠AOB，ON平分∠COD，若∠AOD=70°，∠BOC=10°，则∠MON=
△ABC在方格纸中的位置如图所示，方格纸中的每个小正方形的边长为1个单位，