题目内容
8.一次函数y=kx+4的图象经过点A(-3,-2).(1)求这个一次函数的关系式;
(2)求该函数的图象与坐标轴所围成的三角形的面积.
分析 (1)把A点坐标代入y=kx+4可求出k的值,从而得到一次函数解析式;
(2)先利用坐标轴上点的坐标特征求出一次函数与x轴和y轴的交点坐标,然后根据三角形面积公式求解.
解答 解:(1)把A(-3,-2)代入y=kx+4得-3k+4=-2,解得k=2,
所以这个一次函数解析式为y=2x+4;
(2)当y=0时,2x+4=0,解得x=-2,则直线y=2x+4与x轴的交点坐标为(2,0),
当x=0时,y=2x+4=4,则直线y=2x+4与y轴的交点坐标为(0,4),
所以该函数的图象与坐标轴所围成的三角形的面积=$\frac{1}{2}$×2×4=4.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图所示,从正面看该几何体的图形应为( )
如图所示,从正面看该几何体的图形应为( )
 如图所示,从正面看该几何体的图形应为( )
如图所示,从正面看该几何体的图形应为( )| A. |  | B. |  | C. |  | D. |  |
17.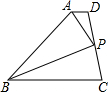 如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )
如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )
 如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )
如图,已知四边形ABCD中,AD∥BC,AP平分∠DAB,BP平分∠ABC,它们的交点P给在线段CD上,下面的结论:①AP⊥BP;②点P到直线AD、BC的距离相等;③PD=PC.其中正确的结论有( )| A. | ①②③ | B. | ①② | C. | 仅① | D. | 仅② |
18.如果单项式-5xa+1y4与2ybx3是同类项,那么a、b的值分别是( )
| A. | a=1,b=4 | B. | a=1,b=3 | C. | a=2,b=4 | D. | a=2,b=3 |
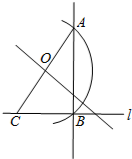 陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图)
陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图)