题目内容
12.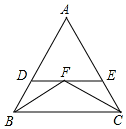 如图,在△ABC中,∠ABC的平分线BF与∠ACB的平分线CF相交于F,过点F作DE∥BC,交直线AB于点D,交直线AC于点E.那么BD,CE,DE之间存在什么数量关系?并证明这种关系.
如图,在△ABC中,∠ABC的平分线BF与∠ACB的平分线CF相交于F,过点F作DE∥BC,交直线AB于点D,交直线AC于点E.那么BD,CE,DE之间存在什么数量关系?并证明这种关系.
分析 结论:BD+CE=DE.只要证明BD=DF,CE=EF,即可解决问题.
解答 解:结论:BD+CE=DE.
理由如下:∵BF、CF分别∠ABC与∠ACB
∴∠ABF=∠CBF,∠ACF=∠BCF
又∵DE∥BC
∴∠BFD=∠CBF,∠CFE=∠BCF
∴∠BFD=∠ABF,∠CFE=∠ACF
∴BD=DF,CE=EF
∴BD+CE=DF+EF=DE.
点评 本题考查等腰三角形的性质和判定,平行线的性质等知识,解题的关键是等腰三角形的证明,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
4.小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相等,小红希望上学时经过每个路口都是绿灯,但实际这样的概率是( )
| A. | 0.125 | B. | 0.5 | C. | 0.375 | D. | 1.5 |
1.圆锥的底面半径是2cm,母线长为6cm,则这个圆锥的侧面展开后得到的扇形圆心角的度数为( )
| A. | 60° | B. | 120° | C. | 45° | D. | 135° |
2.下列运算正确的是( )
| A. | x3+x2=x5 | B. | 2x3•x2=2x6 | C. | (3x3)2=9x6 | D. | x6÷x3=x2 |
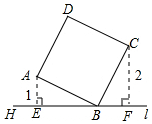 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离AE、CF分别是1cm、2cm,则线段EF的长为3cm.
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离AE、CF分别是1cm、2cm,则线段EF的长为3cm.