题目内容
15．某中学开展植树活动，连续四年共植树1999棵．已知第一年植树344棵，第二年植树500棵．如果第三年和第四年植树棵树的增长率相同，那么该校第三年和第四年各植树多少棵？分析 设后两年年植树棵树的年增长率为x，第一年植树344棵，第二年植树500棵，则第三年植树500（1+x）棵，第四年植树500（1+x）2棵，根据四年累计植树数据列方程求解．
解答 解：设后年植树棵树的年增长率为x，依题意，得
第三年植树500（1+x）棵，第四年植树500（1+x）2棵，
∴四年累计种树为：344+500+500（1+x）+500（1+x）2=1999，
整理，得：100x2+300x-31=0，
解得x1=0.1=10%，x2=-3.1（不合题意舍去）；
第三年植树500×1.1=550棵；
第四年植树500×1.21=605棵；
答：第三年和第四年应植树550棵和605棵．
点评 此题主要考查了一元二次方程的应用，利用增长率相同正确表示出各年份的植树总数，得出等式方程是解题关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
5．
根据如图所示的流程图计算，若输入x的值为-1，则输出y的值为（ ）
根据如图所示的流程图计算，若输入x的值为-1，则输出y的值为（ ）| A． | -2 | B． | -1 | C． | 7 | D． | 17 |
6．点（a-2，b+2）经过平移变换得到点（a，b），则这个平移变换是（ ）
| A． | 先向左平移2个单位长度，再向下平移2个单位长度 | |
| B． | 先向左平移2个单位长度，再向上平移2个单位长度 | |
| C． | 先向右平移2个单位长度，再向下平移2个单位长度 | |
| D． | 先向右平移2个单位长度，再向上平移2个单位长度 |
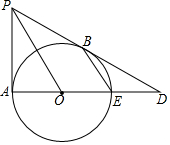如图，PA，PB分别与⊙O相切于点A，B，延长PB交直径AE的延长线于点D．
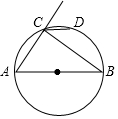如图，AB为⊙O的直径，AB=10，弦AC=6，∠ACB的外角平分线交⊙O于点D，求CD的长．
4．小红和其他2名同学排成一排拍照，则小红排在正中间的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
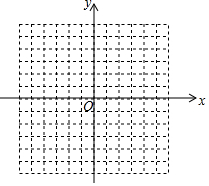如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点（即这些小正方形的顶点）上，且它们的坐标分别是A（2，-3），B（5，-1），C（-1，3），结合所给的平面直角坐标系，解答下列问题：