题目内容
15.若方程$\frac{2x-3}{5}$=$\frac{2}{3}$x-3与3m-$\frac{1}{4}$=3(x+m)-2m的解相同,求(m-3)2的值.分析 先求得方程$\frac{2x-3}{5}$=$\frac{2}{3}$x-3的解,然后将方程的解代入方程3m-$\frac{1}{4}$=3(x+m)-2m得到关于m的一元一次方程,最后解得m的值即可.
解答 解:$\frac{2x-3}{5}$=$\frac{2}{3}$x-3
去分母得:3(2x-3)=10x-45,
去括号得:6x-9=10x-45,
移项得:6x-10x=-45+9,
合并同类项得:-4x=-36
系数化为1得:x=9.
将x=9代入3m-$\frac{1}{4}$=3(x+m)-2m得:3m-$\frac{1}{4}$=3(9+m)-2m,
去分母得:12m-1=12(9+m)-8m,
去括号得:12m-1=108+12m-8m,
移项得:12m-12m+8m=108+1
合并同类项得:8m=109,
系数化为1得:m=$\frac{109}{8}$
∴(m-3)2=$(\frac{109}{8}-3)^{2}$=$(\frac{85}{8})^{2}$=$\frac{7225}{64}$
点评 本题主要考查的是同解方程的定义、解一元一次方程,掌握同解方程的定义是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
5.在平面直角坐标系中,已知点M(1,-4),若将OM绕原点O逆时针旋转180°得到OM1,则点M1所在的位置是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6. 如图,△ABC≌△AED,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )
如图,△ABC≌△AED,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )
 如图,△ABC≌△AED,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )
如图,△ABC≌△AED,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )| A. | 45° | B. | 30° | C. | 60° | D. | 75° |
5.2011年向阳村农民人均收入为7200元,到2013年增长至8712元.这两年中,该村农民人均收入平均每年的增长率为( )
| A. | 10% | B. | 15% | C. | 20% | D. | 25% |
 (1)点C是线段AB上的一点,M、N分别是线段AC、CB的中点.已知AC=4,CB=6.求MN的长.
(1)点C是线段AB上的一点,M、N分别是线段AC、CB的中点.已知AC=4,CB=6.求MN的长.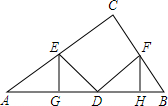 如图,Rt△ABC中,∠C=90°,D点是AB的中点,E、F分别是AC、BC上的两个动点,DE⊥DF,EG⊥AB于G,FH⊥AB于H.
如图,Rt△ABC中,∠C=90°,D点是AB的中点,E、F分别是AC、BC上的两个动点,DE⊥DF,EG⊥AB于G,FH⊥AB于H.
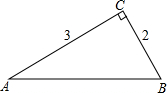 如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA.
如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA.