题目内容
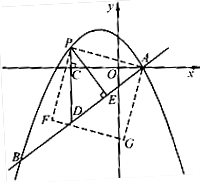
如图,在平面直角坐标系中,直线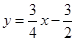 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作如图所示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,求出对应的点P的坐标.
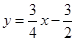 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作如图所示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,求出对应的点P的坐标.
(1) (2)①15 ②
(2)①15 ②
 (2)①15 ②
(2)①15 ②
试题分析:解:(1)对于
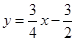 ,当y=0,x=2.当x=—8时,y=—
,当y=0,x=2.当x=—8时,y=— .
.∴A点坐标为(2,0),B点坐标为

由抛物线
 经过A、B两点,得
经过A、B两点,得
解得

(2)①设直线
 与y轴交于点M 当x=0时,y=
与y轴交于点M 当x=0时,y= . ∴OM=
. ∴OM= .
.∵点A的坐标为(2,0),∴OA=2.∴AM=

∵OM:OA:AM=3∶4:5.
由题意得,∠PDE=∠OMA,∠AOM=∠PED=90°,∴△AOM~△PED.
∴DE:PE:PD=3∶4:5.
∵点P是直线AB上方的抛物线上一动点
∴PD=yP-yD
 =
= .
.∴


 ②当点G落在y轴上时
②当点G落在y轴上时由△ACP≌△GOA得PC=AO=2,即
 ,解得
,解得 ,
,所以

点评:该题主要考查学生对观察图形,判断二次函数解析式开口、最值以及求解析式方法的掌握,同时考查在直角坐标系中对几何图形的应用。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
 与x轴交与
与x轴交与 ,
, 两点,
两点,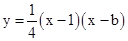 (b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B的左侧),与y轴的正半轴交于点C.
 的自变量x的取值范围是 .
的自变量x的取值范围是 .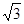 ,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒
,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒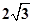 个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒。
个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒。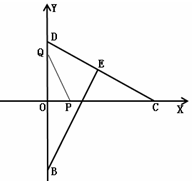
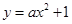 经过P′Q′的中点,此时的抛物线与x轴正半轴交于点M。由已知,直接写出:
经过P′Q′的中点,此时的抛物线与x轴正半轴交于点M。由已知,直接写出: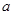 的取值范围为 ;
的取值范围为 ; ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为( ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
 ,BF=
,BF=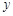 .则
.则