题目内容
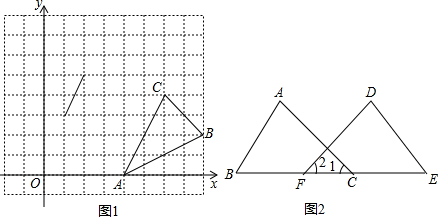
(1)如图1,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0)(8,2),(6,4).已知△A1B1C1的两个顶点的坐标为(1,3),(2,5).若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为
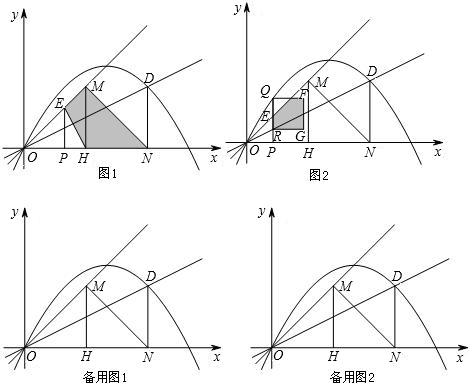
(2)在数学课上,林老师在黑板上画出如图2所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:
证明:
(3,4)或(0,4)
(3,4)或(0,4)
.(2)在数学课上,林老师在黑板上画出如图2所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:
①②③
①②③
;结论:④
④
.(均填写序号)证明:

分析:(1)根据题意画出相应的图形,找出第三个顶点坐标即可;
(2)①②③作为条件,④作为结论,证明:由BF=CE,利用等式的性质两边加上FC得到BC=EF,再由AB=DE,∠B=∠E,利用SAS得出三角形ABC与三角形DEF全等,利用全等三角形对应角相等得到∠1=∠2.
(2)①②③作为条件,④作为结论,证明:由BF=CE,利用等式的性质两边加上FC得到BC=EF,再由AB=DE,∠B=∠E,利用SAS得出三角形ABC与三角形DEF全等,利用全等三角形对应角相等得到∠1=∠2.
解答:
解:(1)如图:第三个顶点坐标为(3,4)或(0,4);
(2)题设:①②③;结论:④,
证明:∵BF=EC,
∴BF+CF=EC+CF,即BC=EF.
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠1=∠2.
故答案为:(1)(3,4)或(0,4);(2)①②③;④

解:(1)如图:第三个顶点坐标为(3,4)或(0,4);
(2)题设:①②③;结论:④,
证明:∵BF=EC,
∴BF+CF=EC+CF,即BC=EF.
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SAS),
∴∠1=∠2.
故答案为:(1)(3,4)或(0,4);(2)①②③;④
点评:此题考查了位似变换,坐标与图形性质,全等三角形的判定与性质,以及命题与性质,弄清题意是解本题的关键.

练习册系列答案
相关题目
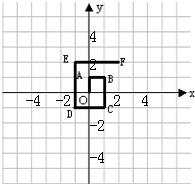 17、如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.①根据图形填表格:
17、如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.①根据图形填表格: