Question

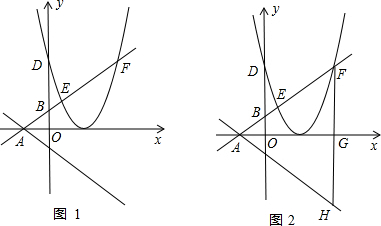
如图1，在平面直角坐标系中，直线l：y=-

3

4

x-

3

2

沿x轴翻折后，与x轴交于点A，与y轴交于点B，抛物线y=

2

3

(x-h)2与y轴交于点D，与直线AB交于点E、点F（点F在点E的右侧）．
（1）求直线AB的解析式；
（2）若线段DF∥x轴，求抛物线的解析式；
（3）如图2，在（2）的条件下，过F作FH⊥x轴于点G，与直线l交于点H，在抛物线上是否存在P、Q两点（点P在点Q的上方），PQ与AF交于点M，与FH交于点N，使得直线PQ既平分△AFH的周长，又平分△AFH面积，如果存在，求出P、Q的坐标，若不存在，请说明理由．

Answer 1

分析：（1）设直线AB的解析式为y=kx+b，先求出直线y=-

3

4

x-

3

2

与x轴、y轴交点坐标，根据沿x轴翻折，得到A、B的坐标，把A、B的坐标代入直线AB的解析式y=kx+b，即可求出直线AB的解析式；
（2）设抛物线的顶点为P（h，0），得出抛物线解析式为：y=

2

3

(x-h)2=

2

3

x2-

4

3

hx+

2

3

h2，根据DF∥x轴，得出F的坐标，把F的坐标代入直线AB的解析式即可求出h的值，即可得到答案；
（3）过M作MT⊥FH于T，得到Rt△MTF∽Rt△AGF，得到FT：TM：FM=FG：GA：FA=3：4：5，设FT=3k，TM=4k，FM=5k，求出FN的值，根据三角形的面积公式求出△MNF和△AFH的面积，根据之间的等量关系即可求出k的值，设直线MN的解析式为：y=kx+b，
把M（

6

5

，

12

5

）、N（6，-4），代入得到方程组，求出方程组的解即可得到直线MN的解析式，解由方程y=-

4

3

x+4和y=

2

3

x²-4x+6的解即可得出P、Q的坐标．

解答：（1）解：设直线AB的解析式为y=kx+b
直线y=-

3

4

x-

3

2

与x轴、y轴交点分别为（-2，0），（0，-

3

2

），
沿x轴翻折，
∵直线y=-

3

4

x-

3

2

，
直线AB与x轴交于同一点（-2，0）
∴A（-2，0）．与y轴的交点（0，-

3

2

）与点B关于x轴对称
∴B（0，

3

2

），
∴

-2k+b=0 b= 3 2 .

解得k=

3

4

，b=

3

2

，
∴直线AB的解析式为 y=

3

4

x+

3

2

．
答：直线AB的解析式为 y=

3

4

x+

3

2

．

（2）解：设抛物线的顶点为Q（h，0），
抛物线解析式为：y=

2

3

(x-h)2=

2

3

x2-

4

3

hx+

2

3

h2，
∴D（0，

2

3

h2 ）．
∵DF∥x轴，
∴点F（2h，

2

3

h2 ），
又点F在直线AB上，∴

2

3

h2=

3

4

•(2h)+

3

2

，
解得 h₁=3，h2=

-3

4

（舍去），
∴抛物线的解析式为y=

2

3

(x-3)2=

2

3

x2-4x+6，
答：抛物线的解析式为y=

2

3

x²-4x+6．

（3）解：过M作MT⊥FH于T，
∴Rt△MTF∽Rt△AGF．
∴FT：TM：FM=FG：GA：FA=3：4：5，
设FT=3k，TM=4k，FM=5k，
则FN=

1

2

(AH+HF+AF)-FM=16-5k，
∴S△MNF=

1

2

FN•MT=

(16-5k)4k

2

，
∵S△AFH=

1

2

FH•AG=

1

2

×12×8=48，
又∵S△MNF=

1

2

S△AFH．
∴

(16-5k)4k

2

=24，
解得k=

6

5

或k=2 （舍去），
∴FM=6，FT=

18

5

，MT=

24

5

，GN=4，TG=

12

5

，
∴M（

6

5

，

12

5

）、N（6，-4），
∴设直线MN的解析式为：y=kx+b，
把M（

6

5

，

12

5

）、N（6，-4），代入得：

12

5

=

6

5

k+b且-4=6k+b，
解得：k=-

4

3

，b=4，
∴y=-

4

3

x+4，
联立y=-

4

3

x+4 与y=

2

3

x2-4x+6，
求得P（1，

8

3

），Q（3，0）．
答：存在P的坐标是（1，

8

3

），Q的坐标是（3，0）．

点评：本题主要考查对用待定系数法求一次函数、二次函数的解析式，解二元一次方程组、解二元二次方程组，三角形相似的性质和判定，图形的旋转等知识点，综合运用这些性质进行计算是解此题的关键，此题是一个拔高的题目，有一定的难度．