题目内容
11.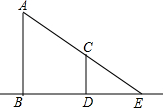 如图,已知小鱼同学的身高(CD)是1.6米,她与树(AB)在同一时刻的影子长分别为DE=2米,BE=5米,那么树的高度AB=4米.
如图,已知小鱼同学的身高(CD)是1.6米,她与树(AB)在同一时刻的影子长分别为DE=2米,BE=5米,那么树的高度AB=4米.
分析 由CD⊥BE、AB⊥BE知CD∥AB,从而得△CDE∽△ABE,由相似三角形的性质有$\frac{CD}{AB}$=$\frac{DE}{BE}$,将相关数据代入计算可得.
解答 解:由题意知CD⊥BE、AB⊥BE,
∴CD∥AB,
∴△CDE∽△ABE,
∴$\frac{CD}{AB}$=$\frac{DE}{BE}$,即$\frac{1.6}{AB}$=$\frac{2}{5}$,
解得:AB=4,
故答案为:4.
点评 本题主要考查相似三角形的应用,熟练掌握相似三角形的判定与性质是解题的关键.

练习册系列答案
相关题目
3.一次函数y=kx+b,当k>0,b<0时,图象经过( )
| A. | 一、二、三象限 | B. | 二、三、四象限 | C. | 一、二、四象限 | D. | 一、三、四象限 |
20.△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
| A. | a:b:c=3:5:6 | B. | a2-c2=b2 | C. | ∠A-∠B=∠C | D. | a=$\sqrt{7}$,b=3,c=4 |
1.下列结论中,正确的是( )
| A. | 把一个角分成两个角的射线叫角平分线 | |
| B. | 两点确定一条直线 | |
| C. | 若AB=BC,则点B是线段AC的中点 | |
| D. | 两点之间,直线最短 |
 如图,面积为1的等腰直角△OA1A2,∠OA2A1=90°,且OA2为斜边在△OA1A2,外作等腰直角△OA2A3,以OA3为斜边在△OA2A3,外作等腰直角△OA3A4,以OA4为斜边在△OA3A4,外作等腰直角△OA4A5,…连接A1A3,A3A5,A5A7,…分别与OA2,OA4,OA6,…交于点B1,B2,B3,…按此规律继续下去,记△OB1A3的面积为S1,△OB2A5的面积为S2,△OB3A7的面积为S3,…△OBnA2n+1的面积为Sn,则Sn=$(\frac{1}{4})^{n-1}×\frac{1}{3}$(用含正整数n的式子表示).
如图,面积为1的等腰直角△OA1A2,∠OA2A1=90°,且OA2为斜边在△OA1A2,外作等腰直角△OA2A3,以OA3为斜边在△OA2A3,外作等腰直角△OA3A4,以OA4为斜边在△OA3A4,外作等腰直角△OA4A5,…连接A1A3,A3A5,A5A7,…分别与OA2,OA4,OA6,…交于点B1,B2,B3,…按此规律继续下去,记△OB1A3的面积为S1,△OB2A5的面积为S2,△OB3A7的面积为S3,…△OBnA2n+1的面积为Sn,则Sn=$(\frac{1}{4})^{n-1}×\frac{1}{3}$(用含正整数n的式子表示).