题目内容
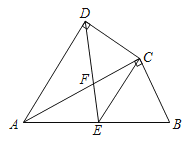
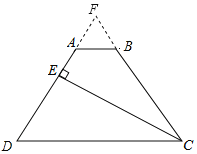
【题目】在梯形ABCD中，AB∥CD，CE平分∠BCD，CE⊥AD于E，DE＝2AE．若△CED面积为1，则四边形ABCE的面积为（ ）
A.
B.
C.
D.
【答案】B
【解析】
延长DA、CB相交于点F，证出∠D=∠F，得出CD=CF，DE=FE，求出AE=AF=
DE，得出
，△CFE的面积=△CDE的面积=1，△FDC的面积=2△CDE的面积=2，证明△FAB∽△FDC，得出S△FAB=
，即可得出答案．
解：如图，延长DA、CB相交于点F，
∵CE平分∠BCD，CE⊥AD，
∴∠D＝∠F，
∴CD＝CF，DE＝FE，
∴△CFE的面积＝△CDE的面积＝1，
∴△FDC的面积＝2△CDE的面积＝2，
∵DE＝2AE，
∴AE＝AF＝DE，
∴，
∵AB∥CD，
∴△FAB∽△FDC，
∴S△FAB＝
S△FDC＝×2＝
，
∴四边形ABCE的面积＝1﹣＝
；
故选：B．
练习册系列答案
相关题目
