题目内容
13.2010年10月9日,我国嫦娥二号卫星进行第三次近月制动,顺利进入离月球表面100km的圆形环月轨道,如图,⊙O代表月球,点P代表嫦娥二号卫星,PC=100km,从点P能看到的月球上最远的点在什么位置?能观察到月球表面的最远距离是多少(月球的直径约为3476km,结果精确到1km)?
分析 连接OA,根据切线的性质和勾股定理计算即可.
解答  解:由题意得,PA、PB切⊙O于A、B,
解:由题意得,PA、PB切⊙O于A、B,
则点A、B是从点P能看到的月球上最远的点,
连接OA,
由题意得,OA=1738km,OP=1738+100=1838km,
由勾股定理得,PA=$\sqrt{O{P}^{2}-O{A}^{2}}$=598km.
点评 本题考查的是切线的性质和勾股定理的应用,掌握圆的切线垂直于过切点的半径是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
4.下列图案是轴对称图形不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列备选答案的四个数中,最小的一个是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
18.下面几个有理数最大的是( )
| A. | 2 | B. | 0 | C. | -3 | D. | -1 |
5.已知∠AOB=70°,∠BOC=30°,OM平分AOB,ON平分∠BOC,则∠MON=( )
| A. | 50° | B. | 20° | C. | 20°或50° | D. | 不能确定 |
3.已知菱形ABCD的边长为5,中心为O,且OA,OB的长是关于x的方程x2+(2m+1)x+m2-4=0的两个实数根,则m的值为( )
| A. | -4 | B. | 2 | C. | -4或2 | D. | 以上都不对 |
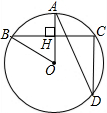 如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上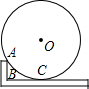 木工师傅可以用角尺测量并计算出圆的半径.如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C.记角尺的直角顶点为B,量得AB=8cm,BC=16cm,则⊙O的半径等于20cm.
木工师傅可以用角尺测量并计算出圆的半径.如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C.记角尺的直角顶点为B,量得AB=8cm,BC=16cm,则⊙O的半径等于20cm.