题目内容
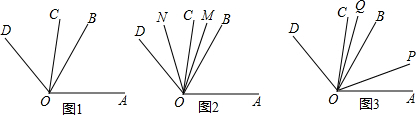
15.已知,如图1,∠AOC=∠BOD=80°.设∠AOC和∠BOD的公共角∠BOC度数是m°(0<m<80).(1)用含m的代数式表示:∠COD的度数是80-m°,∠AOD的度数是160-m°.
(2)若∠AOD=4∠BOC,求m的值.
(3)如图2,当OM、ON分别是∠AOD、∠COD的角平分线时,∠MON的度数是否变化?若不变,求出∠MON的度数;若变化,请说明理由.
(4)若射线OP以每秒10°的速度从OA位置绕点O逆时针运动,同时,射线OQ以每秒5°的速度从OC位置绕点O顺时针运动,当OP在∠AOB内,OQ在∠BOC内时,如图3,在任何某一时刻,总有∠POB=2∠QOB,求m的值.
分析 (1)根据角度的和、差即可求解;
(2)根据(1)以及∠AOD=4∠BOC即可列方程求解;
(3)根据∠MON=$\frac{1}{2}$(∠AOD-∠COD)-$\frac{1}{2}$∠AOC,求得∠MON的度数,即可判断;
(4)设运动的时间是t秒,则∠POB=(80-m)-10t,∠QOB=m-5t,根据PB=2BQ即可列方程求解.
解答 解:(1)∠COD=∠BOD-∠BOC=(80-m)°,
∠AOD=∠COD+∠AOC=80-m+80=160-m°;
故答案是:80-m,160-m;
(2)∵∠AOD=4∠BOC,
∴160-m=4m,
解得:m=32;
(3)∠MON是定值.
理由是:∵OM、ON是∠AOD和∠COD的平分线,
∴∠MOD=$\frac{1}{2}$∠AOD,∠NOD=$\frac{1}{2}$∠COD,
∴∠MON=$\frac{1}{2}$(∠AOD-∠COD)-$\frac{1}{2}$∠AOC=40°,
∴∠MON的度数是定值,是40°;
(4)设运动的时间是t秒,则∠POB=(80-m)-10t,∠QOB=m-5t,
∵PB=2BQ,
∴(80-m)-10t=2(m-5t),
∴m=$\frac{80}{3}$.
点评 本题考查了角度的计算,求角度的方法一般是转化为角的和、差计算.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.下列四个点位于第三象限的是( )
| A. | (1,1) | B. | (4,-2) | C. | (-2,4) | D. | (-1,-2) |
4.下列命题是假命题的是( )
| A. | 如果a∥b,b∥c,那么a∥c | |
| B. | 直角三角形的两个锐角互余 | |
| C. | 两条直线被第三条直线所截,内错角相等 | |
| D. | 两点之间,线段最短 |
 已知如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠A=22.5°,CD=8cm,求⊙O的半径.
已知如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠A=22.5°,CD=8cm,求⊙O的半径.
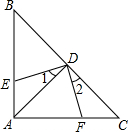 如图,△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF,若AB=8cm,则四边形AEDF的面积为( )
如图,△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF,若AB=8cm,则四边形AEDF的面积为( )