题目内容
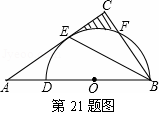
如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边
上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sinA= ,⊙O的半径为4,求图中阴影部分的面积.
,⊙O的半径为4,求图中阴影部分的面积.
 |
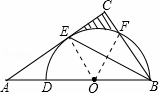
解:(1)连接OE.
∵OB=OE ∴∠OBE=∠OEB
 ∵BE是△ABC的角平分线 ∴∠OBE=∠EBC
∵BE是△ABC的角平分线 ∴∠OBE=∠EBC
∴∠OEB=∠EBC ∴OE∥BC
∵∠C=90° ∴∠AEO=∠C=90°
∴AC是⊙O的切线;
(2)连接OF.
∵sinA=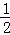 ,∴∠A=30° ∵⊙O的半径为4,∴AO=2OE=8,
,∴∠A=30° ∵⊙O的半径为4,∴AO=2OE=8,
∴AE=4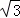 ,∠AOE=60°,∴AB=12, ∴BC=
,∠AOE=60°,∴AB=12, ∴BC=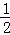 AB=6 AC=6
AB=6 AC=6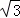 ,
,
∴CE=AC﹣AE=2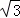 .
.
∵OB=OF,∠ABC=60°,∴△OBF是正三角形.
∴∠FOB=60°,CF=6﹣4=2,∴∠EOF=60°.
∴S梯形OECF=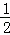 (2+4)×2
(2+4)×2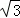 =6
=6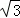 .
.
S扇形EOF=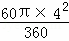 =
=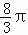
∴S阴影部分=S梯形OECF﹣S扇形EOF=6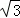 ﹣
﹣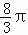 .
.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
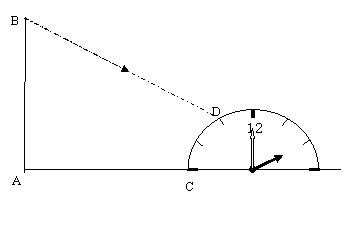
 中,
中, ,
, ,
, .三角板绕直角顶点
.三角板绕直角顶点 逆时针旋转,当点
逆时针旋转,当点 的对应点
的对应点 落在
落在 边的起始位置上时即停止转动,则阴影部分的面积
边的起始位置上时即停止转动,则阴影部分的面积 
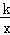 交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=4,则k的值为( )
交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=4,则k的值为( )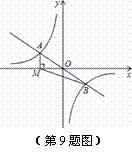
 ,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则:
,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则: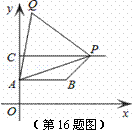
 ,则BF=2;正确的结论有( )
,则BF=2;正确的结论有( )
 (3)设以点P、O、D、E为顶点的四边形面积为y,请直接写出y与x的函数关系式,并写出自变量的取值范围。
(3)设以点P、O、D、E为顶点的四边形面积为y,请直接写出y与x的函数关系式,并写出自变量的取值范围。