题目内容
a、b、c在数轴上的位置如图所示：化简：|a+b|-|c-a|+|b-c|．
考点：整式的加减,数轴,绝对值
专题：
分析：由数轴可知：b＜a＜0＜c，再根据有理数的运算法则，求出绝对值里的代数式的正负性，最后根据绝对值的性质化简．
解答：解：由数轴，得b＜a＜0＜c，
∴a+b＜0，c-a＞0，b-c＜0，
∴|a+b|-|c-a|+|b-c|=
=-a-b-c+a-b+c
=-2b．
故答案为：-2b．
∴a+b＜0，c-a＞0，b-c＜0，
∴|a+b|-|c-a|+|b-c|=
=-a-b-c+a-b+c
=-2b．
故答案为：-2b．
点评：此题考查了整式的加减，绝对值及数轴的应用，做这类题的关键是明确绝对值里的数值是正是负，然后根据绝对值的性质“正数的绝对值是它本身，负数的绝对值是它的相反数，0的绝对值还是0”进行化简计算．
练习册系列答案
挑战100单元检测试卷系列答案
名题金卷系列答案
相关题目
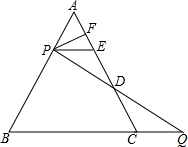如图，△ABC是等边三角形，P是AB上一点，Q是BC延长线上一点，AP=CQ．联结PQ交AC于D点．过P作PE∥BC，交AC于E点．
如图是一个正方体纸盒的两个侧面展开图，请你在其余三个正方体内分别填上适当的数，使得折成正方体后，相对的面上的两个数互为相反数．