题目内容
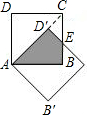
如图，边长为1的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A顺时针旋转45°，则重叠部分的周长________．
2
分析：AD′的延长线一定过点C．则△D′EC是等腰直角三角形，则AB+AD′+BE+BE=2AC，根据勾股定理求得AC的长，即可求解．
解答：
解：延长AD′，
∵∠D′AB=45°，
∴AD′的延长线一定过点C．则△D′EC是等腰直角三角形，则D′E=D′C，
∵正方形的边长是1，则AC=．则AD′+D′E=AC=，
又∵AB=AD′，BE=D′E，
则AB+BE=
∴重叠部分的周长是：AB+AD′+BE+BE=2AC=2．
故答案是：2．
点评：本题考查了正方形的性质，正确理解AD′的延长线一定过点C，则AB+AD′+BE+BE=2AC是关键．
分析：AD′的延长线一定过点C．则△D′EC是等腰直角三角形，则AB+AD′+BE+BE=2AC，根据勾股定理求得AC的长，即可求解．
解答：
解：延长AD′，∵∠D′AB=45°，
∴AD′的延长线一定过点C．则△D′EC是等腰直角三角形，则D′E=D′C，
∵正方形的边长是1，则AC=
．则AD′+D′E=AC=，又∵AB=AD′，BE=D′E，
则AB+BE=
∴重叠部分的周长是：AB+AD′+BE+BE=2AC=2
．故答案是：2
．点评：本题考查了正方形的性质，正确理解AD′的延长线一定过点C，则AB+AD′+BE+BE=2AC是关键．
练习册系列答案
相关题目
附加题
如图，边长为3的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A顺时针旋转45°，则这两个正方形重叠部分的面积是多少？
如图．边长为1的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A顺时针旋转45°，则这两个正方形重叠部分的面积是（ ）
如图，边长为3的两个正方形重合在一起，将其中一个固定不动，另一个绕顶点A旋转45°，求这两个正方形重合部分的面积．
如图，边长为4的两个正方形，则阴影部分的面积为