题目内容
 如图,边长为3的两个正方形重合在一起,将其中一个固定不动,另一个绕顶点A旋转45°,求这两个正方形重合部分的面积.
如图,边长为3的两个正方形重合在一起,将其中一个固定不动,另一个绕顶点A旋转45°,求这两个正方形重合部分的面积.分析:根据题意可以推出△AGM≌△ABM,所以重合部分的面积为2△ABM的面积,进而求出即可.
解答: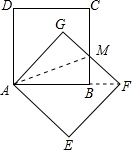 解:连接AM,连接BF,
解:连接AM,连接BF,
∵两个正方形的边长都为3,将其中一个固定不动,另一个绕顶点A旋转45°,
∴A,B,F三点在一条直线上,
∴GAF=∠GFA=45°,
∴MB=BF,
∵AG=AB,AM=AM,
∠G=∠ABM=90°,
∴△AGM≌△ABM,
∴GM=BM,
设BM=x,
∴GM=x,MF=3-x,
∴x2+x2=(3-x)2,
解得:x=-3-3
(不合题意舍去)或x=-3+3
,
∴四边形GABM的面积=2S△ABM=2×
×3×(-3+3
)=9
-9.
 解:连接AM,连接BF,
解:连接AM,连接BF,∵两个正方形的边长都为3,将其中一个固定不动,另一个绕顶点A旋转45°,
∴A,B,F三点在一条直线上,
∴GAF=∠GFA=45°,
∴MB=BF,
∵AG=AB,AM=AM,
∠G=∠ABM=90°,
∴△AGM≌△ABM,
∴GM=BM,
设BM=x,
∴GM=x,MF=3-x,
∴x2+x2=(3-x)2,
解得:x=-3-3
| 2 |
| 2 |
∴四边形GABM的面积=2S△ABM=2×
| 1 |
| 2 |
| 2 |
| 2 |
点评:此题主要考查了正方形的性质定理、三角形的面积、全等三角形的判定和性质.解题关键在于求出BM=BF的长度.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 附加题
附加题
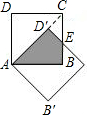
 如图,边长为3的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是多少?
如图,边长为3的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是多少? 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是( )
如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是( ) 如图,边长为4的两个正方形,则阴影部分的面积为
如图,边长为4的两个正方形,则阴影部分的面积为