题目内容
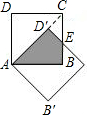
 如图,边长为3的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是多少?
如图,边长为3的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是多少?分析:连接AE,根据旋转性质和正方形性质推出AD′=AD=AB,∠AD'E=∠D=∠B=90°,根据HL证△AD′E和△ABE全等,推出D′E=BE,推出CD′=D′E=BE,设BE=x,求出CE长,得出关于x的方程,求出x的值,根据三角形的面积公式求出即可.
解答:解:连接AE,
因为是绕顶点A顺时针旋转45°角,由旋转的特征和正方形性质可知:
AD′落在AC上,AD′=AD=AB,∠AD′E=∠D=∠B=90°,
在Rt△AD'E和Rt△ABE中:AD′=AB,AE=AE,
∴Rt△AD′E≌Rt△ABE(HL),
∴D′E=BE,
∵AC是正方形对角线,
∴∠D′CE=45°,
∴∠D′EC=45°,
∴D′C=D′E,
设BE=x,则D′C=D′E=x,CE=
=
x,
∴x+
x=3,
解得:x=3(
-1),
S四边形AD′EB=S△ABC-S△CD′E=
×3×3-
×3(
-1)×3(
-1)=9
-9,
答:这两个正方形重叠部分的面积是9
-9.

因为是绕顶点A顺时针旋转45°角,由旋转的特征和正方形性质可知:
AD′落在AC上,AD′=AD=AB,∠AD′E=∠D=∠B=90°,
在Rt△AD'E和Rt△ABE中:AD′=AB,AE=AE,
∴Rt△AD′E≌Rt△ABE(HL),
∴D′E=BE,
∵AC是正方形对角线,
∴∠D′CE=45°,
∴∠D′EC=45°,
∴D′C=D′E,
设BE=x,则D′C=D′E=x,CE=
| D′C2+D′E2 |
| 2 |
∴x+
| 2 |
解得:x=3(
| 2 |
S四边形AD′EB=S△ABC-S△CD′E=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
答:这两个正方形重叠部分的面积是9
| 2 |
点评:本题综合考查了全等三角形性质和判定,三角形的面积,正方形的性质,旋转的性质等知识点的应用,主要培养学生综合运用性质进行推理的能力,本题综合性比较强,有一定的难度,用了方程思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 附加题
附加题
 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是( )
如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是( ) 如图,边长为3的两个正方形重合在一起,将其中一个固定不动,另一个绕顶点A旋转45°,求这两个正方形重合部分的面积.
如图,边长为3的两个正方形重合在一起,将其中一个固定不动,另一个绕顶点A旋转45°,求这两个正方形重合部分的面积. 如图,边长为4的两个正方形,则阴影部分的面积为
如图,边长为4的两个正方形,则阴影部分的面积为