题目内容
13.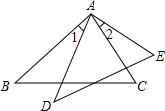 如图所示,AB=AD,AC=AE,∠1=∠2,求证:△ABC≌△ADE.
如图所示,AB=AD,AC=AE,∠1=∠2,求证:△ABC≌△ADE.
分析 已知∠1=∠2,∠DAC是公共角,从而可推出∠DAE=∠BAC,已知AB=AD,AC=AE,从而可以利用SAS来判定△ABC≌△ADE.
解答 证明:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAE}\\{AC=AE}\end{array}\right.$
∴△ABC≌△ADE(SAS).
点评 此题主要考查全等三角形的判定方法,常用的判定方法有:SSS,SAS,AAS,HL等,做题时注意灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下列判定正确的是( )
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 两条对角线相等且互相垂直的四边形是正方形 | |
| C. | 四边相等且有一个角是直角的四边形是正方形 | |
| D. | 一组对边平行,一组对边相等的四边形是平行四边形 |
3.从1,2,3,4,5,6中任意取一个数,取到的数小于3的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
 如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于3.
如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于3.