题目内容
 如图,△ABC中,以BC为直径的半圆交AB于点D,且AC2=AD•AB.
如图,△ABC中,以BC为直径的半圆交AB于点D,且AC2=AD•AB.(1)求证:CA是圆的切线;
(2)O为半圆的圆心,OE⊥BD,已知BE=3,AD=2,求∠B的度数.
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)先根据三角形相似的判定由AC2=AD•AB得到△ACD∽△ABC,则∠ADC=∠ACB,再根据圆周角定理得到∠BDC=90°,所以∠ACB=90°,然后根据切线的判定得到CA是圆的切线;
(2)先根据垂径定理得DE=BE=3,则AB=8,再利用AC2=AD•AB计算出AC,然后根据正弦的定义求∠B的度数.
(2)先根据垂径定理得DE=BE=3,则AB=8,再利用AC2=AD•AB计算出AC,然后根据正弦的定义求∠B的度数.
解答:(1)证明:∵AC2=AD•AB,即
=
,
而∠DAC=∠CAB,
∴△ACD∽△ABC,
∴∠ADC=∠ACB,
∵BC为直径,
∴∠BDC=90°,
∴∠ACB=90°,
∴AC⊥BC,
而C是直径BC的端点,
∴CA是圆的切线;
(2)解:∵OE⊥BD,
∴DE=BE=3,
∴AB=BE+DE+AD=8,
∴AC2=AD•AB=16,
∴AC=4,
在Rt△ABC中,sinB=
=
,
∴∠B=30°.
| AC |
| AD |
| AB |
| AC |
而∠DAC=∠CAB,
∴△ACD∽△ABC,
∴∠ADC=∠ACB,
∵BC为直径,
∴∠BDC=90°,
∴∠ACB=90°,
∴AC⊥BC,
而C是直径BC的端点,
∴CA是圆的切线;
(2)解:∵OE⊥BD,
∴DE=BE=3,
∴AB=BE+DE+AD=8,
∴AC2=AD•AB=16,
∴AC=4,
在Rt△ABC中,sinB=
| AC |
| AB |
| 1 |
| 2 |
∴∠B=30°.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了垂径定理和三角形相似的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若抛物线y=(x-2m)2+3m-1(m是常数)与直线y=x+1有两个交点,且这两个交点分别在抛物线对称轴的两侧,则m的取值范围是( )
| A、m<2 | ||
| B、m>2 | ||
C、m<
| ||
D、m>
|

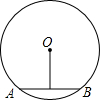 如图,AB是⊙O的一条弦,AB=6,圆心O到AB的距离为4,则⊙O的半径为
如图,AB是⊙O的一条弦,AB=6,圆心O到AB的距离为4,则⊙O的半径为 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针旋转能与△CBP′合,若此时BC平分∠PBP′,PP′交BC于点E,BE=3,求PP′的长.
如图,P是正方形ABCD内一点,将△ABP绕点B顺时针旋转能与△CBP′合,若此时BC平分∠PBP′,PP′交BC于点E,BE=3,求PP′的长.