题目内容
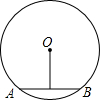如图，AB是⊙O的一条弦，AB=6，圆心O到AB的距离为4，则⊙O的半径为考点：垂径定理,勾股定理
专题：
分析：连接OA，先根据垂径定理求出AD的长，再根据勾股定理即可得出OA的长．
解答：
解：连接OA，
∵AB=6，OD⊥AB，圆心O到AB的距离为4，
∴AD=
AB=3，
∴OA=
=
=5．
故答案为：5．
解：连接OA，∵AB=6，OD⊥AB，圆心O到AB的距离为4，
∴AD=
| 1 |
| 2 |
∴OA=
| AD2+OD2 |
| 32+42 |
故答案为：5．
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
下列事件是随机事件的为（ ）
| A、度量三角形的内角和，结果是180° |
| B、经过城市中有交通信号灯的路口，遇到红灯 |
| C、爸爸的年龄比爷爷大 |
| D、通常加热到100℃时，水沸腾 |
如图，△ABC中，以BC为直径的半圆交AB于点D，且AC2=AD•AB．
如图，已知等腰△ABC的面积为16cm2，点D，E分别是AB，AC边的中点，则梯形DBCE的面为
如图，点G是△ABC的重心，GF∥BC，下列各图中既是轴对称又是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
如图，直线m∥n，∠1=60°，∠2=40°，则∠3的度数为（ ）| A、90° | B、100° |
| C、110° | D、120° |
如图是由一个等腰直角三角形和一个半圆组成的图形．其中AD=CD，点B是线段AC的中点，画出此图关于点B成中心对称的图形．
如图，△ABC按逆时针方向转动了80°后成为△A′B′C′，已知∠B=50°，∠C=65°，那么∠BAC′=