题目内容
5. 抛物线y=-$\frac{4}{9}{x^2}+\frac{8}{3}$x+2与y轴交于点A,顶点为B.点P是x轴上的一个动点,当点P的坐标是($\frac{41}{6}$,0)时,|PA-PB|取得最小值.
抛物线y=-$\frac{4}{9}{x^2}+\frac{8}{3}$x+2与y轴交于点A,顶点为B.点P是x轴上的一个动点,当点P的坐标是($\frac{41}{6}$,0)时,|PA-PB|取得最小值.
分析 根据抛物线的解析式求得A的坐标,顶点B的坐标,设P(x,0),根据当PA=PB是线段PA与PB的差的最小,即可求得最小值和P的坐标.
解答 解:∵抛物线y=-$\frac{4}{9}$x2+$\frac{8}{3}$x+2与y轴交于点A,
∴A(0,2),
∵y=-$\frac{4}{9}$x2+$\frac{8}{3}$x+2=-$\frac{4}{9}$(x-3)2+6,
∴顶点B(3,6),
设P(x,0),
当PA=PB是线段PA与PB的差的最小,PA-PB=0,
∵A(0,2),B(3,6),
∴PA2=x2+22=x2+4,PB2=(x-3)2+62,
∴x2+4=(x-3)2+62,解得:x=$\frac{41}{6}$,
∴当P点坐标为($\frac{41}{6}$,0)时,|PA-PB|取得最小值.
故答案为:($\frac{41}{6}$,0)
点评 本题考查了轴对称-最短路线问题,二次函数的性质等,理解当PA-PB=0时,线段PA与PB的差的最小是关键.

练习册系列答案
相关题目
15.刚刚过去的2017年春运总里程达到12亿千米,约等于地球到太阳距离的8倍,用科学记数法表示12亿为( )
| A. | 1.2×109 | B. | 1.2×108 | C. | 12×109 | D. | 12×108 |
13.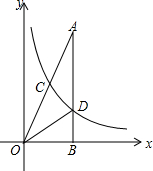 如图,在Rt△AOB中,∠ABO=90°,点B在x轴上,点C(1,a)为OA的中点,反比例函数y=$\frac{k}{x}$的图象经过点C,交AB于点D,且∠AOD=∠BOD,则k=( )
如图,在Rt△AOB中,∠ABO=90°,点B在x轴上,点C(1,a)为OA的中点,反比例函数y=$\frac{k}{x}$的图象经过点C,交AB于点D,且∠AOD=∠BOD,则k=( )
 如图,在Rt△AOB中,∠ABO=90°,点B在x轴上,点C(1,a)为OA的中点,反比例函数y=$\frac{k}{x}$的图象经过点C,交AB于点D,且∠AOD=∠BOD,则k=( )
如图,在Rt△AOB中,∠ABO=90°,点B在x轴上,点C(1,a)为OA的中点,反比例函数y=$\frac{k}{x}$的图象经过点C,交AB于点D,且∠AOD=∠BOD,则k=( )| A. | 8 | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{3}$ |
 问题探究:
问题探究: 如图,在△ABC中,∠ACB=90°,点D在BC边上,且BD=BC,过点B作CD的垂线交AC于点O,以O为圆心,OC为半径画圆.
如图,在△ABC中,∠ACB=90°,点D在BC边上,且BD=BC,过点B作CD的垂线交AC于点O,以O为圆心,OC为半径画圆.