题目内容
13.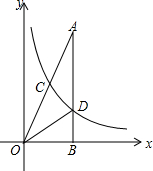 如图,在Rt△AOB中,∠ABO=90°,点B在x轴上,点C(1,a)为OA的中点,反比例函数y=$\frac{k}{x}$的图象经过点C,交AB于点D,且∠AOD=∠BOD,则k=( )
如图,在Rt△AOB中,∠ABO=90°,点B在x轴上,点C(1,a)为OA的中点,反比例函数y=$\frac{k}{x}$的图象经过点C,交AB于点D,且∠AOD=∠BOD,则k=( )| A. | 8 | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{3}$ |
分析 由点C的坐标结合△AOB为直角三角形可得出点A、B的坐标,根据角平分线的性质可得出$\frac{BD}{AD}$=$\frac{OB}{OA}$,由此可得出点D的坐标,再根据反比例函数图象上点的坐标特征即可得出关于a的方程,解之即可得出a、k的值.
解答 解:∵点C(1,a)为OA的中点,
∴点A(2,2a),OA=2$\sqrt{1+{a}^{2}}$.
∵∠ABO=90°,
∴点B(2,0),OB=2,AB=2a.
∵∠AOD=∠BOD,
∴$\frac{BD}{AD}$=$\frac{OB}{OA}$,即BD=$\frac{OB•AD}{OA}$=$\frac{2×(2a-BD)}{2\sqrt{1+{a}^{2}}}$,
∴BD=$\frac{2(\sqrt{1+{a}^{2}}-1)}{a}$,
∴点D(2,$\frac{2(\sqrt{1+{a}^{2}}-1)}{a}$).
∵反比例函数y=$\frac{k}{x}$的图象经过点C、D,
∴k=1×a=2×$\frac{2(\sqrt{1+{a}^{2}}-1)}{a}$,
整理得:$\sqrt{1+{a}^{2}}$=3,
解得:a=2$\sqrt{2}$或a=-2$\sqrt{2}$(舍去),
∴k=a=2$\sqrt{2}$.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征、直角三角形以及角平分线,用含a的代数式表示出点D的坐标是解题的关键.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a5 | C. | 2-3=-6 | D. | 20=1 |
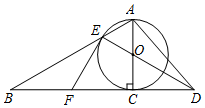 如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.
如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD. 如图,弦BE与弦CD交于点G,点E为$\widehat{DC}$的中点,过点B的直线交DC延长线于点A,AB∥DE.
如图,弦BE与弦CD交于点G,点E为$\widehat{DC}$的中点,过点B的直线交DC延长线于点A,AB∥DE.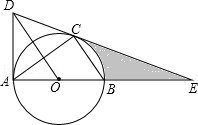 如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①b2-4ac<0;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③2a+b=0;④当y>0时,x的取值范围是-1<x<3;⑤当x>0时,y随x增大而减小.其中结论正确的个数是( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①b2-4ac<0;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③2a+b=0;④当y>0时,x的取值范围是-1<x<3;⑤当x>0时,y随x增大而减小.其中结论正确的个数是( ) 抛物线y=-$\frac{4}{9}{x^2}+\frac{8}{3}$x+2与y轴交于点A,顶点为B.点P是x轴上的一个动点,当点P的坐标是($\frac{41}{6}$,0)时,|PA-PB|取得最小值.
抛物线y=-$\frac{4}{9}{x^2}+\frac{8}{3}$x+2与y轴交于点A,顶点为B.点P是x轴上的一个动点,当点P的坐标是($\frac{41}{6}$,0)时,|PA-PB|取得最小值. 某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/时=$\frac{50}{3}$米/秒)
某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/时=$\frac{50}{3}$米/秒)