题目内容
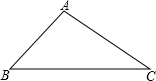 某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌.
某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌. (1)请帮助小敏同学计算广告牌的面积;
(2)你认为小敏同学的意见正确吗?说说你的看法.
考点:圆的综合题
专题:探究型
分析:(1)作△ABC的外接圆⊙O,连接OA、OB,如图1,根据圆周角定理可得∠AOB=60°,从而可得到△OAB是等边三角形,就可得到⊙O的半径,就可解决问题.
(2)易得△ABC是钝角三角形,以钝角所对的边为直径圆能将该三角形覆盖,通过计算就可得到以BC为直径的圆⊙O′是将△ABC完全覆盖且面积最小的圆.
(2)易得△ABC是钝角三角形,以钝角所对的边为直径圆能将该三角形覆盖,通过计算就可得到以BC为直径的圆⊙O′是将△ABC完全覆盖且面积最小的圆.
解答:解:(1)作△ABC的外接圆⊙O,连接OA、OB,如图1.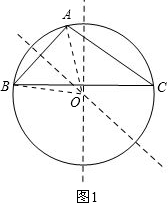
∵∠C=30°,
∴∠AOB=2∠C=60°.
∵OA=OB,
∴△OAB是等边三角形,
∴OA=OB=AB=4,
∴S⊙O=π•OA2=16π.
∴小敏同学设计广告牌的面积为16π平方米.
(2)我认为小敏同学的意见不正确.
∵∠B=45°,∠C=30°,
∴∠BAC=105°,
∴△ABC是钝角三角形,
∴以BC为直径的圆⊙O′可以将△ABC完全覆盖.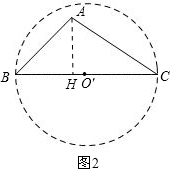
过点A作AH⊥BC于H,
∵AB=4,∠B=45°,∠AHB=90°,
∴AH=AB•sinB=4×
=2
,
BH=AB•cosB=4×
=2
,
在Rt△AHC中,
∵tanC=
,∠C=30°,AH=2
,
∴HC=2
,
∴BC=BH+HC=2
+2
,
∴O′B=
+
,
∴S⊙O′=π•O′B2=π×(
+
)2=(8+4
)π.
∵
<2,∴4
<8,
∴8+4
<16,
∴S⊙O′<S⊙O,
∴以BC为直径的圆⊙O′是将△ABC完全覆盖且面积最小的圆.

∵∠C=30°,
∴∠AOB=2∠C=60°.
∵OA=OB,
∴△OAB是等边三角形,
∴OA=OB=AB=4,
∴S⊙O=π•OA2=16π.
∴小敏同学设计广告牌的面积为16π平方米.
(2)我认为小敏同学的意见不正确.
∵∠B=45°,∠C=30°,
∴∠BAC=105°,
∴△ABC是钝角三角形,
∴以BC为直径的圆⊙O′可以将△ABC完全覆盖.

过点A作AH⊥BC于H,
∵AB=4,∠B=45°,∠AHB=90°,
∴AH=AB•sinB=4×
| ||
| 2 |
| 2 |
BH=AB•cosB=4×
| ||
| 2 |
| 2 |
在Rt△AHC中,
∵tanC=
| AH |
| HC |
| 2 |
∴HC=2
| 6 |
∴BC=BH+HC=2
| 2 |
| 6 |
∴O′B=
| 2 |
| 6 |
∴S⊙O′=π•O′B2=π×(
| 2 |
| 6 |
| 3 |
∵
| 3 |
| 3 |
∴8+4
| 3 |
∴S⊙O′<S⊙O,
∴以BC为直径的圆⊙O′是将△ABC完全覆盖且面积最小的圆.
点评:本题主要考查了圆周角定理、等边三角形的判定与性质、锐角三角函数、圆的面积公式等知识,由本题可以总结以下经验:能够将锐角三角形(或直角三角形)完全覆盖的最小的圆是该三角形的外接圆,能够将钝角三角形完全覆盖的最小的圆是以钝角所对的边为直径的圆.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,点A、B的坐标分别为(-1,3)、(-4,1),先将线段AB沿一确定方向平移得到线段A1B1,点A的对应点为A1,点B1的坐标为(0,2),在将线段A1B1绕原点O顺时针旋转90°得到线段A2B2,点A1的对应点为点A2.
如图,在平面直角坐标系中,点A、B的坐标分别为(-1,3)、(-4,1),先将线段AB沿一确定方向平移得到线段A1B1,点A的对应点为A1,点B1的坐标为(0,2),在将线段A1B1绕原点O顺时针旋转90°得到线段A2B2,点A1的对应点为点A2. 如图,∠AOB=30°,P是角平分线上的点,PM⊥OB于点M,PN∥OB交OA于点N,若PM=1,则PN=
如图,∠AOB=30°,P是角平分线上的点,PM⊥OB于点M,PN∥OB交OA于点N,若PM=1,则PN=