题目内容
求证:不论m为何值,关于x的方程2x2+(m+8)x+m+5=0一定有两个不相等的实数根.
考点:根的判别式
专题:证明题
分析:要证明方程总有两个不相等的实数根,那么只要证明△>0即可.
解答:证明:∵a=2,b=m+8,c=m+5,
∴△=(m+8)2-4×2(m+5)
=m2+16m+64-8m-40
=m2+8m+24
=(m+4)2+8>0,
∴不论m为任何实数,方程总有两个不相等的实数根.
∴△=(m+8)2-4×2(m+5)
=m2+16m+64-8m-40
=m2+8m+24
=(m+4)2+8>0,
∴不论m为任何实数,方程总有两个不相等的实数根.
点评:本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
 小明同学从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小明同学从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息: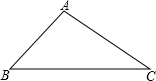 某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌.
某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌.