题目内容
 如图,在平面直角坐标系中,点A、B的坐标分别为(-1,3)、(-4,1),先将线段AB沿一确定方向平移得到线段A1B1,点A的对应点为A1,点B1的坐标为(0,2),在将线段A1B1绕原点O顺时针旋转90°得到线段A2B2,点A1的对应点为点A2.
如图,在平面直角坐标系中,点A、B的坐标分别为(-1,3)、(-4,1),先将线段AB沿一确定方向平移得到线段A1B1,点A的对应点为A1,点B1的坐标为(0,2),在将线段A1B1绕原点O顺时针旋转90°得到线段A2B2,点A1的对应点为点A2.(1)画出线段A1B1、A2B2;
(2)求在这两次变换过程中,点A经过的路线的长度;
(3)求在这两次变换过程中线段AB所扫过的面积.
考点:作图-旋转变换,弧长的计算,扇形面积的计算,作图-平移变换
专题:作图题
分析:(1)根据网格结构找出点A、B平移后的对应点A1、B1的位置,然后连接即可;再找出点A2、B2的位置,然后连接即可;
(2)利用勾股定理列式求出AA1,OA1,再利用弧长公式列式计算即可得解;
(3)根据AB扫过的面积等于平行四边形的面积加上两个扇形的面积的差,列式计算即可得解.
(2)利用勾股定理列式求出AA1,OA1,再利用弧长公式列式计算即可得解;
(3)根据AB扫过的面积等于平行四边形的面积加上两个扇形的面积的差,列式计算即可得解.
解答: 解:(1)线段A1B1、A2B2如图所示;
解:(1)线段A1B1、A2B2如图所示;
(2)由勾股定理得,AA1=
=
,
OA1=
=5,
点A经过的路线的长度=
+
=
+
π;
(3)AB向右平移3个单位,向上平移1个单位,
AB平移到A1B1扫过的面积=3×1=3,
线段A1B1旋转到A2B2所扫过的面积=
=
π,
所以,这两次变换过程中线段AB所扫过的面积为
π+3.
 解:(1)线段A1B1、A2B2如图所示;
解:(1)线段A1B1、A2B2如图所示;(2)由勾股定理得,AA1=
| 12+42 |
| 17 |
OA1=
| 32+42 |
点A经过的路线的长度=
| 17 |
| 90•π•5 |
| 180 |
| 17 |
| 5 |
| 2 |
(3)AB向右平移3个单位,向上平移1个单位,
AB平移到A1B1扫过的面积=3×1=3,
线段A1B1旋转到A2B2所扫过的面积=
| 90•π•52 |
| 360 |
| 25 |
| 4 |
所以,这两次变换过程中线段AB所扫过的面积为
| 25 |
| 4 |
点评:本题考查了利用旋转变换作图,利用平移变化作图,弧长的计算,扇形的面积,难点在于(3)中线段扫过的面积的计算.

练习册系列答案
相关题目
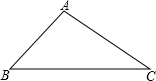 某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌.
某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌. 