题目内容
已知b<c<0<a,则|a|+|a-c|-2|c-b|+|a+b|= .
考点:整式的加减,绝对值
专题:
分析:分为两种情况:①当a+b≥0时,②当a+b<0时,去掉绝对值符号,再合并同类项即可.
解答:解:①当a+b≥0时,∵b<c<0<a,
∴|a|+|a-c|-2|c-b|+|a+b|
=a+a-c-2(c-b)+a+b
=a+a-c-2c+2b+a+b
=3a+3b-3c;
②当a+b<0时,∵b<c<0<a,
∴|a|+|a-c|-2|c-b|+|a+b|
=a+a-c-2(c-b)-a-b
=a+a-c-2c+2b-a-b
=a+b-3c,
故答案为:3a+3b-3c或a+b-3c.
∴|a|+|a-c|-2|c-b|+|a+b|
=a+a-c-2(c-b)+a+b
=a+a-c-2c+2b+a+b
=3a+3b-3c;
②当a+b<0时,∵b<c<0<a,
∴|a|+|a-c|-2|c-b|+|a+b|
=a+a-c-2(c-b)-a-b
=a+a-c-2c+2b-a-b
=a+b-3c,
故答案为:3a+3b-3c或a+b-3c.
点评:本题考查了整式的加减,绝对值的应用,解此题的关键是能正确去掉绝对值符号.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 如图,上午8时一条船从A出发(60海里/时)向正东航行,8时30分到B处,经测小岛M在A北偏东45°,在B北偏东30°方向,那么BM的距离为( )
如图,上午8时一条船从A出发(60海里/时)向正东航行,8时30分到B处,经测小岛M在A北偏东45°,在B北偏东30°方向,那么BM的距离为( )A、20(
| ||
B、30
| ||
C、15(
| ||
D、30(
|
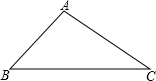 某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌.
某公司临街的外墙上有一块三角形的墙面(如图所示)发生破损现象,公司领导让工人师傅做一个圆形广告牌,将破损面全部覆盖住,工人师傅量的∠B=45°,∠C=30°,AB=4m,考虑到成本问题,应使所做的广告牌尽可能小,同学晓敏认为,作△ABC的外接圆,即可能得到满足要求的广告牌. 
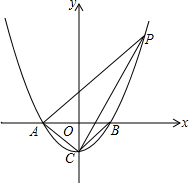 如图,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C
如图,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C