题目内容
17. 在一堂关于“折纸问题”的数学综合实践探究课中,小明同学将一张矩形ABCD纸片,按如图进行折叠:分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF对对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF,且边C′E与A′B交于点G,边A′F与C′D交于一点H.已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=1,则矩形纸片ABCD的周长为62.
在一堂关于“折纸问题”的数学综合实践探究课中,小明同学将一张矩形ABCD纸片,按如图进行折叠:分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF对对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF,且边C′E与A′B交于点G,边A′F与C′D交于一点H.已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=1,则矩形纸片ABCD的周长为62.
分析 延长BA′交DE于M,作MN⊥C′D于N,由矩形的性质得出∠A=∠C=90°,AD=BC,AB=CD,由折叠的性质得出∠C′=∠C=90°,∠A′=∠A=90°,CE=C′E,AB=A′B,∠CDE=∠C′DE,∠CED=∠C′ED,∠ABF=∠A′BF,∠AFB=∠A′FB,由SAS证明△ABF≌△CDE(SAS),得出∠ABF=∠CDE,∠CED=∠AFB,由ASA证明△BEG≌△DFH,得出∠BGE=∠DHF,证出四边形MNC′G是矩形,得出MN=C′G=1,∠GMN=90°,设EG=3x,BG=4x,则BE=5x,CE=C′E=3x+1,CD=AB=A′B=4x+6,由三角函数求出DN=$\frac{3}{4}$,由勾股定理得出DM=$\frac{5}{4}$,再由三角函数得出方程,解方程求出x=2,得出AB=CD=14,AD=BC=17,即可得出矩形ABCD的周长.
解答 解:延长BA′交DE于M,作MN⊥C′D于N,如图所示:
∵四边形ABCD是矩形,
∴∠A=∠C=90°,AD=BC,AB=CD,
由折叠的性质得:∠C′=∠C=90°,∠A′=∠A=90°,CE=C′E,AB=A′B,∠CDE=∠C′DE,∠CED=∠C′ED,∠ABF=∠A′BF,∠AFB=∠A′FB,
在△ABF和△CDE中,
$\left\{\begin{array}{l}{AB=CD}&{\;}\\{∠A=∠C}&{\;}\\{AF=CE}&{\;}\end{array}\right.$,
∴△ABF≌△CDE(SAS),
∴∠ABF=∠CDE,∠CED=∠AFB,
∴∠BEG=∠DFH,∠EBG=∠FDH,
∵CE=AF,
∴BE=DF,
在△BEG和△DFH中,
$\left\{\begin{array}{l}{∠BEG=∠DFH}&{\;}\\{BE=DF}&{\;}\\{∠EBG=∠FDH}&{\;}\end{array}\right.$,
∴△BEG≌△DFH(ASA),
∴∠BGE=∠DHF,
∵∠A′GC′=∠BGE,∠A′HC′=∠DHF,
∴∠BGE=∠DHF=∠A′HC′=∠A′GC′=(360°-90°-90°)÷2=90°,
∴四边形MNC′G是矩形,
∴MN=C′G=1,∠GMN=90°,
∴∠DMN=∠EBG,
∵tan∠EBG=$\frac{3}{4}$,
∴设EG=3x,BG=4x,则BE=5x,
∴CE=C′E=3x+1,CD=AB=A′B=4x+6,
∵tan∠DMN=$\frac{DN}{MN}$=tan∠EBG=$\frac{3}{4}$,MN=1,
∴DN=$\frac{3}{4}$,
∴DM=$\frac{5}{4}$,
∵tan∠EBG=$\frac{CM}{BC}$=$\frac{3}{4}$,
即$\frac{4x+6-\frac{5}{4}}{3x+1+5x}$,解得:x=2,
∴AB=CD=14,AD=BC=17,
∴矩形ABCD的周长=2(14+17)=62.
故答案为:62.
点评 本题考查了矩形的性质、翻折变换的性质、全等三角形的判定与性质、勾股定理、三角函数等知识;本题综合性强,难度较大,证明三角形全等是解决问题的关键.

| 劳动时间(小时) | 2 | 3 | 4 |
| 人数 | 3 | 2 | 1 |
| A. | 中位数是2 | B. | 众数是2 | C. | 平均数是3 | D. | 方差是0 |
| A. | $\frac{1}{2016}$ | B. | -2016 | C. | -$\frac{1}{2016}$ | D. | 2016 |
 如图,边长相等的正方形、正六边形的一边重合,则∠1的度数为( )
如图,边长相等的正方形、正六边形的一边重合,则∠1的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 如图,AB是⊙O的直径,点C、D是⊙O上的两点,若BC∥DO,∠D=35°,则∠A的度数是( )
如图,AB是⊙O的直径,点C、D是⊙O上的两点,若BC∥DO,∠D=35°,则∠A的度数是( )| A. | 20° | B. | 15° | C. | 10° | D. | 25° |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
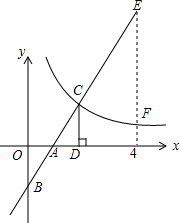 如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论:
如图,在直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: