题目内容
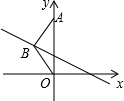 如图,等腰三角形ABO中,底边OA在y轴的正半轴上,且OA=3,点B在第二象限.若直线y=-
如图,等腰三角形ABO中,底边OA在y轴的正半轴上,且OA=3,点B在第二象限.若直线y=-| 1 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点:两条直线相交或平行问题,等腰三角形的性质
专题:
分析:过点B作BE⊥x轴于点E,则OE=
OA=
,得到点B的纵坐标为
,再根据直线y=-
x+1恰好经过点B,求出点B的横坐标,得到BE的长,再求面积即可.
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答:解:过点B作BE⊥x轴于点E,则OE=
OA=
,

∴点B的纵坐标为
,
∵直线y=-
x+1经过点B,
∴
=-
x+1,x=-1.
∴BE=1,
∴△ABO的面积是:
OA×BE=
×3×1=
.
故选:B.
| 1 |
| 2 |
| 3 |
| 2 |

∴点B的纵坐标为
| 3 |
| 2 |
∵直线y=-
| 1 |
| 2 |
∴
| 3 |
| 2 |
| 1 |
| 2 |
∴BE=1,
∴△ABO的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选:B.
点评:本题主要考查了两条直线相交以及等腰三角形的性质.关键是得到点B的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数据:2,5,4,5,3,4,4的众数与中位数分别是( )
| A、4,3 | B、4,4 |
| C、3,4 | D、4,5 |
二次根式
中字母x的取值范围是( )
| x-1 |
| A、x<1 | B、x≤1 |
| C、x>1 | D、x≥1 |

 如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.