题目内容
7.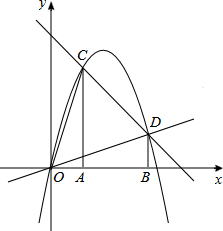 如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.
如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由.
分析 (1)先确定出点C,D的坐标,再用待定系数法求出抛物线解析式,
(2)根据题意设出点M的坐标,表示出点N坐标,以A、C、M、N为顶点的四边形为平行四边形只要AC=MN,用它建立方程求出m即可.
解答 解:(1)∵过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点,
∴点C(1,3),D(3,1),
∵抛物线y=ax2+bx+c经过O、C、D三点,
∴c=0,a+b=3,9a+3b=1.
∴a=-$\frac{4}{3}$,b=$\frac{13}{3}$,c=0,
∴抛物线解析式为y=-$\frac{4}{3}$x2+$\frac{13}{3}$x,
(2)∵A(1,0),C(1.3),
∴AC=3,
∵AC⊥x轴,MN⊥x轴,
∴AC∥MN,
∵以A、C、M、N为顶点的四边形为平行四边形,
∴AC=MN,
∵点D坐标为(3,1),
∴直线OD解析式为y=$\frac{1}{3}$x,
∵点M为直线OD上的一个动点,
∴设M(m,$\frac{1}{3}$m),
∴N(m,-$\frac{4}{3}$m2+$\frac{13}{3}$m),
∴MN=|-$\frac{4}{3}$m2+$\frac{13}{3}$m-$\frac{1}{3}$m|=$\frac{1}{3}$|4m2-12m|,
∵AC=MN,
∴$\frac{1}{3}$|4m2-12m|=3,
∴|4m2-12m|=9,
①当4m2-12m>0时,即m<0,或m>4,
∴4m2-12m=9,
∴m=$\frac{3±3\sqrt{2}}{2}$,
∴点M的横坐标为$\frac{3+3\sqrt{2}}{2}$或$\frac{3-3\sqrt{2}}{2}$,
②当4m2-12m<0时,即0<m<4,
∴4m2-12m=-9,
∴m=$\frac{3}{2}$,
即:存在符合条件的点M,求此时点M的横坐标为$\frac{3+3\sqrt{2}}{2}$或$\frac{3-3\sqrt{2}}{2}$或m=$\frac{3}{2}$.
点评 此题是二次函数综合题,主要考查了待定系数法求抛物线解析式,平行四边形的性质,绝对值方程,用待定系数法求抛物线解析式是解本题的关键.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | (-2,0) | B. | (-2,1) | C. | (2,0) | D. | (2,1) |
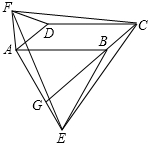 如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:
如图,在?ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论: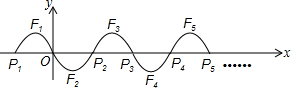 如图,在平面直角坐标系xOy中,二次函数y=-x2-2x图象位于x轴上方的部分记作F1,与x轴交于点P1和O;F2与F1关于点O对称,与x轴另一个交点为P2;F3与F2关于点P2对称,与x轴另一个交点为P3;….这样依次得到F1,F2,F3,…,Fn,则Fn的顶点坐标为[2n-3,(-1)n+1](n为正整数,用含n的代数式表示).
如图,在平面直角坐标系xOy中,二次函数y=-x2-2x图象位于x轴上方的部分记作F1,与x轴交于点P1和O;F2与F1关于点O对称,与x轴另一个交点为P2;F3与F2关于点P2对称,与x轴另一个交点为P3;….这样依次得到F1,F2,F3,…,Fn,则Fn的顶点坐标为[2n-3,(-1)n+1](n为正整数,用含n的代数式表示).


 如图,将边长为1个单位长度的正方形ABCD置于平面直角坐标系内,如果BC与x轴平行,且点A的坐标是(2,2),那么点C的坐标为(3,1).
如图,将边长为1个单位长度的正方形ABCD置于平面直角坐标系内,如果BC与x轴平行,且点A的坐标是(2,2),那么点C的坐标为(3,1).