题目内容
9.若$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{c}{|c|}$=-1,则$\frac{ab}{{|{ab}|}}$+$\frac{{|{bc}|}}{bc}$+$\frac{ac}{{|{ac}|}}$=-1.分析 根据绝对值的性质,可化简绝对值.
解答 解:由$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{c}{|c|}$=-1,得
a>0,b<0,c<0;a<0,b>0,c<0;a<0,b<0,c>0,
当a>0,b<0,c<0时,$\frac{ab}{{|{ab}|}}$+$\frac{{|{bc}|}}{bc}$+$\frac{ac}{{|{ac}|}}$=-1+1-1=-1;
当a<0,b>0,c<0时,$\frac{ab}{{|{ab}|}}$+$\frac{{|{bc}|}}{bc}$+$\frac{ac}{{|{ac}|}}$=-1-1+1=-1;
当a<0,b<0,c>0时,$\frac{ab}{{|{ab}|}}$+$\frac{{|{bc}|}}{bc}$+$\frac{ac}{{|{ac}|}}$=1-1-1=-1,
故答案为:-1.
点评 本题考查了绝对值,利用绝对值的性质是解题关键.

练习册系列答案
相关题目
 如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E.F分别为AC和AB的中点,则EF=3.
如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E.F分别为AC和AB的中点,则EF=3.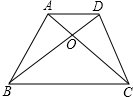 如图,已知梯形ABCD的面积为S,AD∥BC,BC=b,AD=a(a<b),对角线AC与BD交于点O.若△COD的面积为$\frac{2}{9}$S,则$\frac{a}{b}$=$\frac{1}{2}$.
如图,已知梯形ABCD的面积为S,AD∥BC,BC=b,AD=a(a<b),对角线AC与BD交于点O.若△COD的面积为$\frac{2}{9}$S,则$\frac{a}{b}$=$\frac{1}{2}$.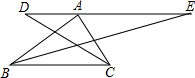 如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于E,D.若AC=6,AB=8,则∠DOE=135°,DE的长为14.
如图,在Rt△ABC中,∠BAC=90°,过顶点A的直线DE∥BC,∠ABC,∠ACB的平分线分别交DE于E,D.若AC=6,AB=8,则∠DOE=135°,DE的长为14.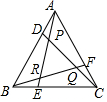 如图,若△ABC为等边三角形,且AD=BE=CF,则∠PQR的度数是60°.
如图,若△ABC为等边三角形,且AD=BE=CF,则∠PQR的度数是60°.