题目内容
6.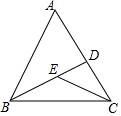 如图,已知在△ABC中,BD是角平分线,点E在BD上,连接CE,若∠BCE=25°,∠CED=55°,则∠ABC的度数为( )
如图,已知在△ABC中,BD是角平分线,点E在BD上,连接CE,若∠BCE=25°,∠CED=55°,则∠ABC的度数为( )| A. | 30° | B. | 40° | C. | 60° | D. | 70° |
分析 G根据三角形的外角的性质得到∠CBE,然后根据角平分线的定义即刻得到结论.
解答 解:∵∠BCE=25°,∠CED=55°,
∴∠CBE=∠CED-∠BCE=55°-25°=30°,
∵BD是角平分线,
∴∠ABC=2∠CBE=60°,
故选C.
点评 本题考查了三角形的外角的性质,角平分线的定义,熟练掌握外角的性质是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
18.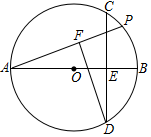 已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
 已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )| A. | $\frac{\sqrt{3}}{3}$π | B. | $\sqrt{3}$ | C. | $\frac{2}{3}$π | D. | 2 |
15.下列各式的计算结果中,不正确的是( )
| A. | x+4x=5x | B. | 3ab-2ab=ab | C. | -5x2y+7xy2=2x2y | D. | 4m+2n-(n-m)=5m+n |
 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用26米长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x米.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用26米长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x米.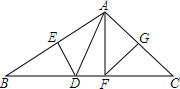 如图,已知在△ABC中,AB=6,AC=5,DE垂直平分AB,FG垂直平分AC,连接AD,AF.
如图,已知在△ABC中,AB=6,AC=5,DE垂直平分AB,FG垂直平分AC,连接AD,AF.