Question

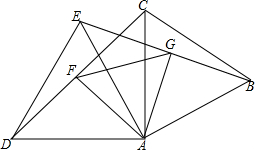如图，已知△ABC和△ADE均为等边三角形，连接CD、BE，作AF⊥CD于点F，AG⊥BE于点G，求证：△AFG为等边三角形．

Answer 1

考点：全等三角形的判定与性质,等边三角形的判定与性质

专题：证明题

分析：根据等边三角形的性质得出AD=AE，AC=AB，∠DAE=∠CAB=60°，求出∠DAC=∠EAB，证△DAC≌△EAB，推出∠AEB=∠ADC，证△AFD≌△AGE，推出AF=AG，∠DAF=∠EAG，求出∠FAG=∠DAE=60°，根据等边三角形的判定推出即可．

解答：证明：∵△ABC和△ADE均为等边三角形，
∴AD=AE，AC=AB，∠DAE=∠CAB=60°，
∴∠DAE+∠EAC=∠CAB+∠EAC，
即∠DAC=∠EAB，
在△DAC和△EAB中

AD=AE ∠DAC=∠EAB AC=AB

，
∴△DAC≌△EAB，
∴∠AEB=∠ADC，
∵AF⊥DC，AG⊥BE，
∴∠AFD=∠EGA=90°，
在△ADF和△AEG中

∠AFD=∠AGE ∠ADF=∠AEG AD=AE

∴△AFD≌△AGE，
∴AF=AG，∠DAF=∠EAG，
∴∠DAF+∠FAE=∠EAG+∠FAE，
即∠FAG=∠DAE=60°，
∴△AFG为等边三角形．

点评：本题考查了等边三角形的性质和判定，全等三角形的性质和判定的应用，主要考查学生的推理哪里，题目比较好，难度适中．