题目内容
关于x的二次多项式a(x3+x2+3x)+b(2x2+x)+x3-5,当x=1时的值是-10,求当x=-1时,该多项式的值是 .
考点:代数式求值
专题:计算题
分析:把x=1代入多项式,使其值为-10,得到关系式,再将x=-1代入计算即可求出值.
解答:解:二次多项式a(x3+x2+3x)+b(2x2+x)+x3-5=(a+1)x3+(a+2b)x2+(3a+b)x-5,
得到a+1=0,即a=-1,
原式=(2b-1)x2+(b-3)x-5,
令x=1,得到2b-1+b-3-5=-10,即b=-
,
则x=-1时,原式=2b-1+3-b-5=b-3=-3
.
故答案为:-3
得到a+1=0,即a=-1,
原式=(2b-1)x2+(b-3)x-5,
令x=1,得到2b-1+b-3-5=-10,即b=-
| 1 |
| 3 |
则x=-1时,原式=2b-1+3-b-5=b-3=-3
| 1 |
| 3 |
故答案为:-3
| 1 |
| 3 |
点评:此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
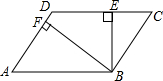 如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=2,DF=1,∠EBF=60°,则这个?ABCD的面积是( )
如图,?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E、F,CE=2,DF=1,∠EBF=60°,则这个?ABCD的面积是( )A、2
| ||
B、2
| ||
C、3
| ||
D、12
|
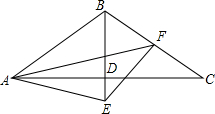 如图,△ABC中,AB=BC,∠B=120°,作AC的垂直平分线交AC于D点,点E在BD的延长线上,连接AE,作∠BAE的角平分线交BC于F,求∠AFE的大小.
如图,△ABC中,AB=BC,∠B=120°,作AC的垂直平分线交AC于D点,点E在BD的延长线上,连接AE,作∠BAE的角平分线交BC于F,求∠AFE的大小.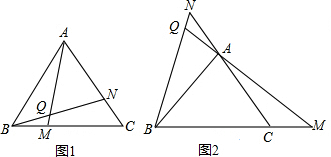
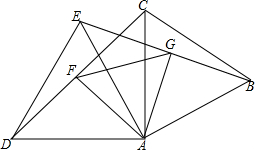 如图,已知△ABC和△ADE均为等边三角形,连接CD、BE,作AF⊥CD于点F,AG⊥BE于点G,求证:△AFG为等边三角形.
如图,已知△ABC和△ADE均为等边三角形,连接CD、BE,作AF⊥CD于点F,AG⊥BE于点G,求证:△AFG为等边三角形.